
2. Теорема Жордана для случая многоугольников
Теорема Жордана утверждает, что всякая простая замкнутая кривая С разделяет точки плоскости, не принадлежащие С, на такие две области (не имеющие общих точек), по отношению к которым сама кривая С является общей границей. Мы докажем здесь эту теорему для частного случая, когда С есть замкнутый многоугольник Р.
Мы покажем, что точки плоскости (кроме точек, находящихся на самом многоугольном контуре Р) разбиваются на два класса A и В, обладающие следующими свойствами: 1) две точки одного и того же класса могут быть соединены ломаной линией, не имеющей общих точек с Р; 2) если две точки принадлежат разным классам, то любая ломаная линия, их соединяющая, имеет общие точки с P. Один из названных классов образует "внутренность" многоугольника, другой - состоит из точек, находящихся "вне" многоугольника.
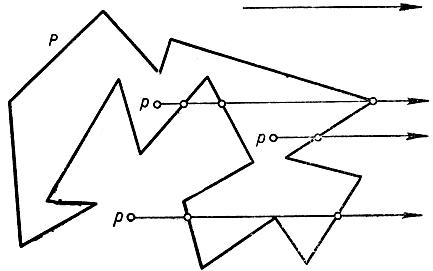
Рис. 148. Счет пересечений
Приступая к доказательству, выберем какое-то фиксированное направление в нашей плоскости, не параллельное ни одной из сторон Р. Так как Р имеет конечное число сторон, то это всегда возможно. Затем определим классы А и В следующим образом.
Точка р принадлежит классу Ф, если луч, проведенный через нее в фиксированном направлении, пересекает Р в четном числе точек (0, 2, 4, 6 и т. д.). Точка р принадлежит классу В, если луч, проведенный из р в фиксированном направлении, пересекает Р в нечетном числе точек (1, 3, 5 и т. д.).
К этому нужно добавить, что если рассматриваемый луч проходит через какую-нибудь вершину Р, то эта вершина идет в счет как точка пересечения луча с Р или не идет, смотря по тому, расположены ли прилежащие стороны многоугольника Р по разные стороны луча или по одну и ту же его сторону.
Условимся говорить, что две точки р и q имеют одну и ту же "четность", если они принадлежат одному и тому же из двух классов А и В.
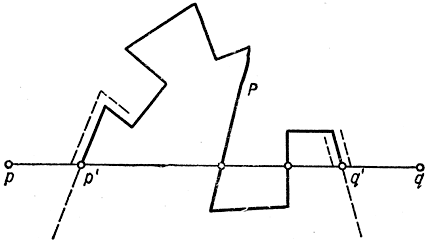
Рис. 149. К доказательству теоремы Жордана
Заметим прежде всего, что все точки любого отрезка прямой, не пересекающегося с Р, имеют одну и ту же четность. Действительно, четность точки р, движущейся по такому отрезку, может измениться не иначе, как при пересечении соответствующего луча с одной из вершин Р; но, принимая во внимание наше соглашение о счете точек пересечения, легко убедиться, что в каждом из двух возможных случаев четность все же не меняется. Из сказанного следует, что если некоторая точка р1 области А соединена ломаной линией с некоторой точкой р2 области В, то эта линия непременно пересекает Р. Иначе четность всех точек ломаной линии, в частности точек р1 и р2, была бы одинаковой. Дальше, покажем, что две точки одного и того же из двух классов A и В могут быть соединены ломаной линией, не пересекающейся с Р. Обозначим две данные точки через р и q. Если прямолинейный отрезок pq, соединяющий р и q, не пересекается с Р, то доказывать больше нечего. В противном случае пусть р' - первая, aq - последняя точка пересечения отрезка pq с многоугольником Р (рис. 149). Построим ломаную линию, начинающуюся от точки р прямолинейным отрезком, расположенным по направлению pq, но заканчивающуюся непосредственно перед точкой р'; отсюда ломаная пойдет вдоль Р (безразлично, в каком из двух возможных направлений) и будет так идти, пока не придет снова на прямую pq около точки q . Весь вопрос в том, произойдет ли пересечение с прямой pq на отрезке р'q или на отрезке q'q: мы сейчас убедимся, что справедливо именно последнее, и тогда будем иметь возможность закончить ломаную, соединяя последнюю из полученных точек с точкой q прямолинейным отрезком, снова лежащим на отрезке pq. Если две точки г и s расположены очень близко одна от другой, но по разные стороны одной из сторон многоугольника Р, то они имеют различную четность, так как выходящие из них (в фиксированном направлении) лучи будут таковы, что на одном из них будет на одну точку больше точек пересечения с Р, чем на другом. Отсюда ясно, что четность меняется, когда, двигаясь по pq, мы проходим через точку q . Значит, ломаный "путь", намеченный на чертеже пунктиром, вернется на pq между q' и q, так как р и q (следовательно, все точки на рассматриваемом "пути") имеют одну и ту же четность.
Таким образом, теорема Жордана для случая многоугольника доказана. "Внешними" по отношению к многоугольнику Р будут те точки, которые принадлежат классу А: действительно, двигаясь по какому-нибудь лучу в фиксированном направлении достаточно далеко, мы, несомненно, придем к точке, за которой пересечений с Р уже не будет, и все такие точки будут принадлежать классу А, так что их четность будет 0. Тогда уже придется заключить, что точками "внутренними" будут точки класса В. Каким бы запутанным ни был замкнутый многоугольник Р, всегда очень легко узнать, расположена ли данная точка р внутри или вне его: достаточно из р провести луч и посчитать число его точек пересечения с Р. Если это число нечетное, значит, р "сидит" внутри и не сможет выбраться наружу, не пересекая Р. Но если это число четное, то точка р - вне многоугольника Р (попробуйте проверить это на рис. 128).
Вот идея другого доказательства жордановой теоремы для случая многоугольников. Определим порядок точки р0 относительно замкнутой кривой С (не проходящей через р0) как число полных поворотов*, совершаемых стрелкой (вектором), проведенным от р к р0, когда точка р делает один обход по кривой С.
* (Это число нужно, конечно, брать в алгебраическом смысле, т. е. с учетом направления вращения (ср. определение индекса на стр. 283).)
Затем пусть А есть совокупность точек р0 (не на Р) четного порядка относительно Р, а В есть совокупность точек р0(не на Р) нечетного порядка относительно Р. В таком случае А и В, определенные указанным способом, представляют собой соответственно области "внешнюю" и "внутреннюю" относительно Р. Читатель может в качестве упражнения воспроизвести все детали доказательства.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'