*2. Эйлерова характеристика поверхности

Предположим, что замкнутая поверхность S рода р разбита на некоторое число областей: такое подразделение получается, если мы отметим на S ряд "вершин" и соединим их затем между собой дугами кривых. Мы покажем, что в таком случае

где V - число вершин, Е - число дуг и F - число областей. Число 2-2р называется эйлеровой характеристикой поверхности. Как мы уже видели, для случая сферы V - Е + F = 2, что согласуется с формулой (1), так как сфера имеет род р, равный нулю.

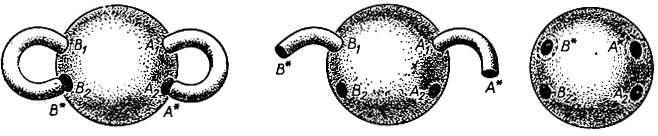
Рис. 138. К эйлеровой характеристике поверхностей

Желая доказать общую формулу (1), вообразим, что S есть сфера с р рукоятками. Как мы отметили, любая поверхность рода р может быть непрерывной деформацией приведена к этому виду, и во время деформации ни V - Е + F, ни 2-2р не изменяются. Непрерывную деформацию мы выберем таким образом, чтобы замкнутые кривые А₁, A₂, В₁, В₂, ..., по которым рукоятки соединяются со сферой, пришлись как раз на дуги данного разбиения. (Рис. 138 иллюстрирует описываемую дальше процедуру в случае р = 2.)

Прорежем теперь поверхность S по кривым A₂, В₂, ... и выпрямим рукоятки. У каждой рукоятки появится свободный край, ограниченный новой кривой A^*, В^*, ..., причем на появившемся крае будет столько же вершин и столько же дуг, сколько их было соответственно на А₂, В₂, ... .

Число V - Е + F при разрезе не изменится, так как новых областей не возникнет, а число вновь возникших вершин уравновешивается числом вновь возникших дуг. Затем деформируем поверхность дальше, сплющивая торчащие рукоятки (включая их в поверхность сферы). В итоге получается сфера с 2р отверстиями. Так как V - Е + F, как нам известно, равно 2 для всякого разбиения полной сферы, то для нашей сферы с 2р отверстиями мы получаем V - Е + F = 2-2p, и это равенство, очевидно, справедливо также и для первоначальной сферы с р рукоятками. Наше утверждение доказано.

Рис. 121 иллюстрирует применение формулы (1) к поверхности S, составленной из плоских многоугольников. Эту поверхность можно топологически деформировать в поверхность тора, так что ее род р равен 1, и потому 2 - 2р = 2 - 2 = 0. Как и требуется по формуле (1), мы получаем:

Упражнение. Произвести какое-нибудь разбиение на поверхности с двумя дырами, изображенной на рис. 137, и проверить, что V - E + F = -2.