§ 4. Топологическая классификация поверхностей

1. Род поверхности

Многие простые, но весьма существенные обстоятельства выясняются при изучении двумерных поверхностей. Сравним, например, поверхность сферы с поверхностью тора. Взглянув на рис. 135, сразу можно обнаружить различие: на сфере, как и на плоскости, замкнутая кривая вроде С разделяет поверхность на две части; но на торе существуют и такие замкнутые кривые, например С, которые не разделяют поверхности на две части. Если мы говорим, что кривая С разделяет сферу на две части, то это означает, другими словами, что при разрезании поверхности сферы по кривой С эта поверхность распадается на два не связанных между собой куска, или, еще иначе, что можно найти две такие точки сферы, что всякая кривая на сфере, их соединяющая, непременно пересечется с кривой С. Напротив, если разрезать тор по кривой С, то после разреза поверхность не распадется: любые две ее точки можно соединить кривой, не имеющей общих точек с С. Указанное различие свидетельствует о том, что сфера и тор в топологическом смысле не принадлежат одному и тому же классу поверхностей: тор нельзя топологически преобразовать в сферу.

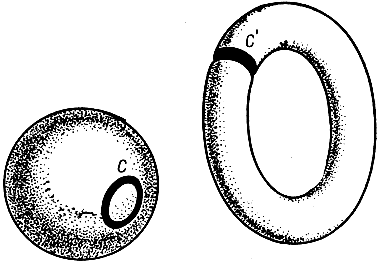
Рис. 135. Разрезы на сфере и на торе

Рассмотрим теперь поверхность с двумя "дырами", изображенную на рис. 136. На этой поверхности оказывается возможным провести сразу две замкнутые кривые A и B, которые не разделяют поверхности на части. Тор, напротив, при проведении двух таких кривых непременно разделится на части. С другой стороны, любые три замкнутые кривые разделяют нашу поверхность с двумя дырами.

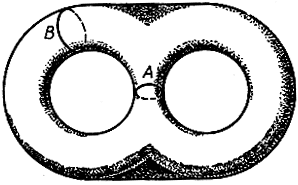
Рис. 136. Поверхность рода 2

Все это подсказывает мысль ввести понятие рода поверхности, понимая под родом поверхности наибольшее возможное число взаимно не пересекающихся простых замкнутых кривых, которые можно провести на поверхности, не разделяя ее на части. Род сферы равен 0, род тора равен 1, род поверхности, изображенной на рис. 136, равен 2. Такая же поверхность с р "дырами" имеет род р. Род есть топологический инвариант поверхности: он не изменяется при деформировании поверхности. Обратно, можно доказать (но мы не приводим здесь этого доказательства), что если две замкнутые поверхности имеют один и тот же род, то одну можно деформировать в другую; таким образом, род р = 0, 1, 2, ... замкнутой поверхности полностью характеризует топологический класс, к которому она принадлежит. (Здесь предполагается, что мы рассматриваем только обыкновенные "двусторонние" поверхности. В пункте 3 этого параграфа мы рассмотрим также и "односторонние" поверхности.) Например, только что рассмотренная поверхность с двумя "дырами" и сфера с двумя "рукоятками", изображенная на рис. 137, являются обе замкнутыми поверхностями рода 2, и мы видим, что каждую из этих поверхностей удается деформировать в другую. Так как поверхность с р дырами или ее эквивалент - сфера с р рукоятками - поверхности рода р, то любую из этих поверхностей можно взять в качестве "топологического представителя" всех замкнутых поверхностей рода р.

Рис. 137. Поверхности рода 2