2. Свойства связности

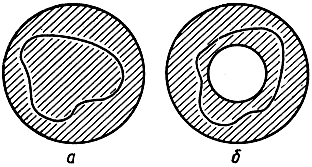
Рис. 125. Односвязная и двусвязная области

В качестве следующего примера фигур, топологически неэквивалентных, рассмотрим две плоские области, изображенные на рис. 125. Первая состоит из внутренних точек круга; вторая - из всех точек, расположенных между двумя концентрическими окружностями. Любая замкнутая кривая, лежащая в области а, может быть непрерывно деформирована или "сжата" в одну точку, не выходя из этой области. Область, обладающая таким свойством, называется односвязной. Что касается области b, то она не односвязна. Так, окружность, концентрическая с двумя граничными окружностями и лежащая между ними, не может быть сжата в точку, не выходя из области, так как во время деформации кривая должна будет пройти через общий центр кругов, а он не принадлежит рассматриваемой области. Область, которая не является односвязной, называется многосвязной. Если двусвязную область b разрезать вдоль одного из радиусов, как это показано на рис. 126, то полученная область окажется одно-связной.

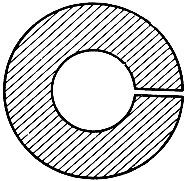
Рис. 126. После разреза двусвязная область становится односвязной

Вообще, можно построить области с двумя, тремя или большим количеством "дыр". Область с двумя "дырами" изображена на рис. 127; чтобы превратить ее в односвязную, нужно сделать два разреза. Если нужно сделать n-1 взаимно не пересекающихся разрезов от границы к границе, чтобы превратить данную многосвязную область в одно-связную, то говорят, что область имеет порядок связности n. Порядок связности плоской области представляет собой важный топологический инвариант этой области.

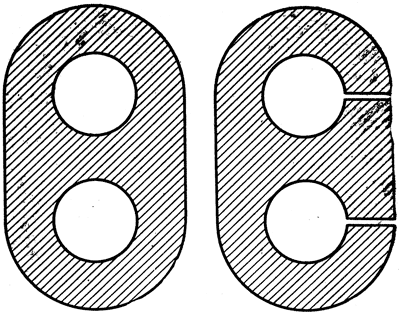
Рис. 127. Редукция трехсвязной области