§ 2. Топологические свойства фигур

1. Топологические свойства

Мы установили, что формула Эйлера справедлива для случая любого простого многогранника. Но эта формула не теряет смысла и значимости также и применительно к иным, гораздо более общим случаям: вместо многогранников элементарной геометрии с плоскими гранями и прямыми ребрами можно взять простые "многогранники", у которых "гранями" будут кривые поверхности, а "ребрами" - кривые линии, или можно нарисовать "грани" и "ребра" на поверхности, например, шара. Больше того, вообразим, что поверхность многогранника или сферы сделана из тонкого слоя резины; тогда формула Эйлера сохраняет силу, как бы ни была деформирована рассматриваемая поверхность - путем изгибаний, сжатий, растяжений и т. д., лишь бы резиновый слой не был порван. Действительно, формула Эйлера относится только к числу вершин, ребер и граней; длины же, площади, двойные отношения, кривизна и т. п., как и иные понятия элементарной или проективной геометрии, в данном случае никакой роли не играют.

Мы уже указывали, что элементарная геометрия имеет дело с величинами (расстояния, углы, площади), которые не меняют своих значений при движениях рассматриваемых фигур, тогда как проективная геометрия занимается такими понятиями (точка, прямая, отношение инцидентности, двойное отношение), которые сохраняются при более широкой группе проективных преобразований. Однако и движения, и проективные преобразования - только очень частные случаи гораздо более общих топологических преобразований; топологическое преобразование одной геометрической фигуры A в другую А' определяется как произвольное соответствие р↔р между точками р фигуры А и точками р' фигуры A", обладающее следующими свойствами:

1. Взаимной однозначностью. (Это значит, что каждой точке р фигуры А сопоставлена одна и только одна точка р' фигуры A', и обратно.)
2. Взаимной непрерывностью. (Это значит, что если мы возьмем две точки р и q фигуры А и станем двигать р так, чтобы расстояние между р и q неограниченно уменьшалось, то расстояние между соответствующими точками р' и q' фигуры A' также будет неограниченно уменьшаться, и обратно.)

Всякое свойство геометрической фигуры A, которое сохраняется также и для той фигуры А', в которую А переходит при топологическом преобразовании, называется топологическим свойством фигуры A; топология же - это та отрасль геометрии, которая рассматривает исключительно топологические свойства фигур. Представьте себе, что некоторая фигура должна быть скопирована от руки совершенно малоопытным, но очень добросовестным чертежником, который невольно искривляет прямые линии, искажает углы, расстояния и площади; тогда на сделанной им копии, хотя метрические и проективные свойства фигуры, может быть, и не сохранятся, но топологические свойства все же останутся в неприкосновенности.

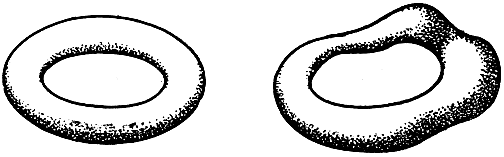
Рис. 123. Поверхности, топологически эквивалентные

Наиболее наглядными примерами топологических преобразований могут служить деформации. Вообразите, что фигура вроде сферы или треугольника сделана из тонкого слоя резины (или нарисована на таковом), и затем растягивайте и крутите резину самыми разнообразными способами, лишь бы не рвать ее и не приводить двух различных точек в состояние физического совпадения. (Приведение двух различных точек в состояние физического совпадения нарушило бы условие 1. Разрыв резинового слоя противоречил бы условию 2: действительно, рассматривая две точки, лежащие по разные стороны линии разрыва, мы видим, что расстояние между ними может быть неограниченно малым, тогда как после разрыва этого уже не будет.)

Рис. 124. Поверхности, топологически неэквивалентные

Фигура в окончательном ее положении - после указанных операций - будет находиться в топологическом соответствии с фигурой в ее первоначальном положении. Треугольник можно деформировать в другой треугольник или в окружность, или в эллипс, и потому названные фигуры обладают совершенно одинаковыми топологическими свойствами. Но никак нельзя деформировать круг в отрезок прямой или поверхность сферы в боковую поверхность цилиндра.

Но общее понятие топологического преобразования шире, чем понятие деформации. Например, если фигура разрезана до деформации и склеена по тем же линиям после деформации, то в итоге, несомненно, получается некоторое топологическое преобразование первоначальной фигуры, хотя это преобразование может и не быть деформацией. Так, две кривые, изображенные на рис. 134 (стр. 286), топологически эквивалентны друг другу и эквивалентны каждая окружности, так как их можно разрезать, распутать и снова склеить. Но предварительно не разрезав, невозможно одну кривую деформировать в другую.

Топологические свойства фигур (вроде того свойства, которое дается теоремой Эйлера, или других, которые будут рассмотрены ниже) представляют величайший интерес во многих математических исследованиях. В известном смысле это самые глубокие, самые основные геометрические свойства, так как они сохраняются при самых "резких" преобразованиях.