§ 1. Формула Эйлера для многогранников

Хотя в античной геометрии изучение многогранников занимало одно из центральных мест, только Декарту и Эйлеру было суждено открыть следующее предложение: Пусть V - число вершин простого многогранника, Е - число ребер, F - число граней: тогда

Под многогранником здесь подразумевается тело, поверхность которого состоит из конечного числа граней, имеющих форму многоугольников. В случае правильных многогранников все многоугольники конгруэнтны и все плоские углы при вершинах равны между собой. Многогранник называется простым, если в нем нет "дыр", так что посредством непрерывной деформации его поверхность может быть переведена в поверхность сферы. На рис. 120 изображен простой многогранник, который не является правильным; на рис. 121 изображен многогранник, не являющийся простым.

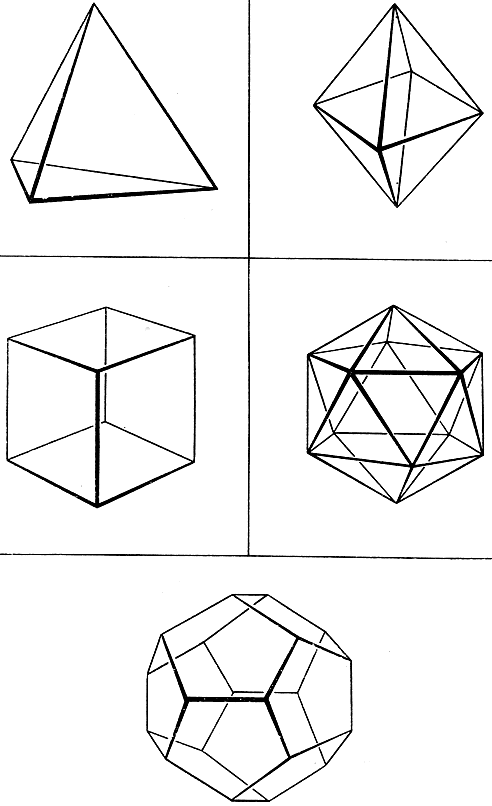
Рис. . Правильные многогранники

Предлагаем читателю проверить справедливость формулы Эйлера для всех многогранников, представленных на рис. 119 и 120; но пусть он убедится также, что для многогранника на рис. 121 эта формула неверна.

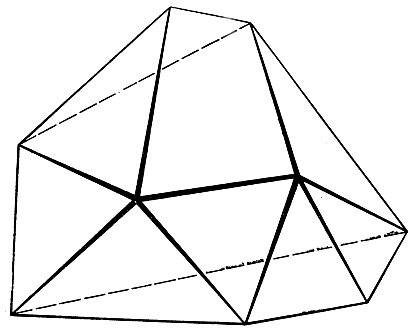
Рис. 120. Простой многогранник: V - E + F = 9 - 18 + 11 = 2

Переходя к доказательству формулы Эйлера, вообразим, что наш многогранник внутри пустой и что поверхность его сделана из тонкой резины. Тогда, вырезав предварительно одну из граней пустого внутри многогранника, можно оставшуюся поверхность деформировать таким образом, что она расстелется по плоскости. Конечно, при этом и грани многогранника и углы между ребрами испытают резкие изменения. Но "сетка", составленная из вершин и ребер на плоскости, будет содержать то же число вершин и ребер, что и первоначальный многогранник, тогда как число граней станет на одну меньше, так как одна грань была вырезана. Мы убедимся теперь, что для полученной нами сетки на плоскости будет справедливо равенство V - Е + F = 1; тогда, добавляя вырезанную грань, для первоначального многогранника получим равенство V - Е + F = 2.

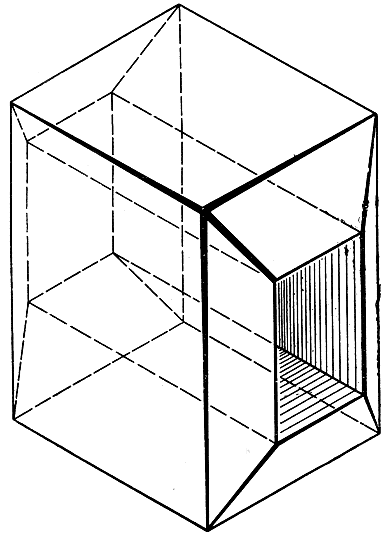
Рис. 121. Непростой многогранник: V - E + F = 16 - 32 + 16 = 0

Прежде всего "триангулируем" плоскую сетку следующим образом. Если в сетке имеются многоугольники с числом углов, большим трех, то, выбрав один из них, проведем в нем какую-нибудь диагональ. В результате каждое из чисел Е и F увеличится на единицу, но значение выражения V - Е + F от этого не изменится. Будем и дальше проводить диагонали, соединяя пары точек (рис. 122), пока сетка не окажется состоящей из одних только треугольников (в чем и заключается наша ближайшая цель). В триангулированной сетке величина V - Е + F имеет то же значение, какое имела и до триангуляции, так как проведение каждой новой диагонали этого значения не меняет. Некоторые из треугольников, далее, имеют ребра (проще сказать - стороны), принадлежащие к "границе" триангулированной сетки. Некоторые из этих треугольников (например, aВС) имеют лишь одно ребро на границе, другие - по два. Возьмем один из такого рода "граничных" треугольников и удалим из,него все то, что не принадлежит какому-либо другому треугольнику. Так, в треугольнике AВС удалим ребро AС и саму грань, оставляя вершины А, В, С и ребра AВ и ВС, но в треугольнике DEF удалим грань, два ребра DF и FE и вершину F. При "уничтожении" таких треугольников, как AВС, числа Е и F уменьшаются на 1, а V не изменяется, так что V - Е + F также не изменяется. При уничтожении треугольников типа DEF V уменьшается на 1, Е на 2 и F на 1, так что опять-таки V - Е + F не изменяется. Последовательное осуществление таких удалений граничных треугольников (причем всякий раз меняется и сама граница) приводит, наконец, к одному-единственному треугольнику, имеющему, очевидно, три ребра, три вершины и одну грань. Для образуемой им совсем простой сетки V - Е + F = 3 - 3 + 1 = 1. Но мы видели, что при удалении из сетки каждого треугольника V - Е + F не изменялось. Значит, V - Е + F должно было равняться единице и для первоначальной плоской сетки, а также для того многогранника с вырезанной гранью, из которого была получена плоская сетка. Отсюда следует, что для исходного многогранника (до вырезания грани) должно было иметь место равенство V - Е + F = 2. Этим и завершается доказательство теоремы Эйлера.

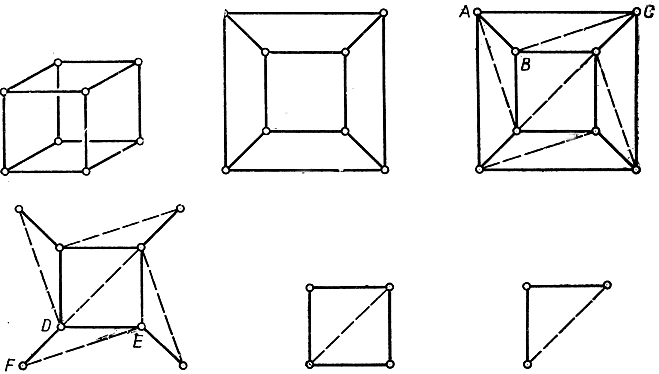
Рис. 122. Доказательство теоремы Эйлера

С помощью теоремы Эйлера легко показать, что существует не более пяти типов правильных многогранников. Предположим, что правильный многогранник имеет F граней, из которых каждая есть правильный n-угольник, и что y каждой вершины сходится r ребер. Считая ребра один раз по граням, другой - по вершинам, получим, во-первых,

(так как каждое ребро принадлежит, двум граням и, следовательно, считается дважды в произведении n) и, во-вторых.

(так как каждое ребро упирается в две вершины). Тогда равенство Эйлера (1) нам дает

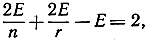
или

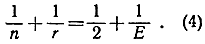
Заметим прежде всего, обращаясь к рассмотрению последнего соотношения, что n≥3 и r≥3, так как многоугольник имеет не меньше трех сторон и в каждой вершине сходится не менее трех граней. С другой стороны, оба числа n и r не могут быть более 3, так как в противном случае левая часть равенства (4) не превышала бы ¹/₂ и равенство было бы невозможно ни при каком положительном значении Е. Итак, нам остается выяснить, какие значения может принять r, если n = 3, и какие значения может принять - n, если r = 3. Подсчитав все возникающие возможности, мы получим число типов правильных многогранников.

При n = 3 равенство (4) принимает вид:

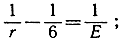
r может здесь равняться 3, 4 или 5 (6 или большее значение исключается, так как 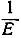положительно.) При этих значениях n и r оказывается, что Е соответственно равно 6, 12 или 30. Так получаются многогранники: тетраэдр, октаэдр и икосаэдр.

Таким же образом при r = 3 равенство (4) принимает вид:

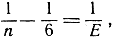
из которого следует, что n = 3, 4 или 5 и соответственно E = 6, 12 или 30.Получаются многогранники: тетраэдр, куб и додекаэдр.

Подставляя полученные значения n, r и Е в соотношения (2) и (3), мы установим число вершин V и число граней F соответствующих многогранников.