*3. Геометрический, или комбинаторный, подход

Хотя аналитический подход к n-мерной геометрии чрезвычайно прост и удобен для многих приложений, все же следует упомянуть и о другом методе, носящем чисто геометрический характер. Он основан на редукции n-мерных данных к (n-1)-мерным, что открывает возможность определять многомерные геометрии посредством математической индукции.

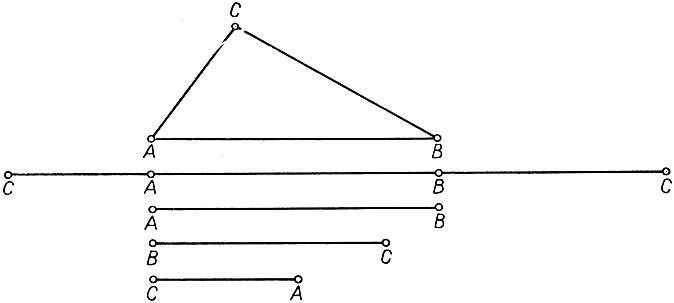
Рис. 116. Определение треугольника по сторонам с сопоставленными друг другу концами

Начнем с того, что рассмотрим контур треугольника ABC в двух измерениях. Разрезая его в точке С и затем поворачивая стороны АС и ВС соответственно около А и В, мы выпрямим контур в прямолинейный отрезок (рис. 116), на котором точка С будет фигурировать дважды. Полученная одномерная фигура дает исчерпывающее представление контура двумерного треугольника. Сгибая фигуру в точках А и В и добившись совпадения двух точек С, мы имеем возможность восстановить треугольник. Но важно то, что сгибать вовсе и не нужно. Достаточно условиться, что мы "идентифицируем" (т. е. не будем различать) обе точки С, несмотря на то что эти две точки и не совпадают в обычном смысле. Можно сделать еще следующий шаг: разрезая фигуру также и в точках А и В, мы получим три отрезка СA, АВ, ВС, которые при желании можно опять сложить таким образом, чтобы был восстановлен "настоящий" треугольник ABC, причем пары идентифицируемых точек совпадут между собой. Идея идентифицировать различные точки в данной совокупности отрезков, чтобы из них построить многоугольный контур (в нашем случае - треугольник), практически иногда оказывается очень полезной. Если нужно отправить в дальнее путешествие какое-нибудь соединение из металлических балок, например мостовую ферму, то удобнее всего упаковать сложенные вместе, предварительно разъединенные балки, обозначив одними и теми же знаками те концы различных балок, которые должны быть соединены вместе. Такое собрание балок с размеченными концами совершенно эквивалентно пространственной конструкции. Предыдущее замечание приводит к мысли о том, как можно "разнять" двумерный многогранник в трехмерном пространстве, заменяя его фигурами низших измерений. Возьмем, например, поверхность куба (рис. 117). Ее сейчас же можно свести к системе из шести квадратов, стороны которых надлежащим образом идентифицированы; следующий шаг будет состоять в том, чтобы заменить эту систему квадратов системой из 12 прямолинейных отрезков с надлежащим образом идентифицированными концами.

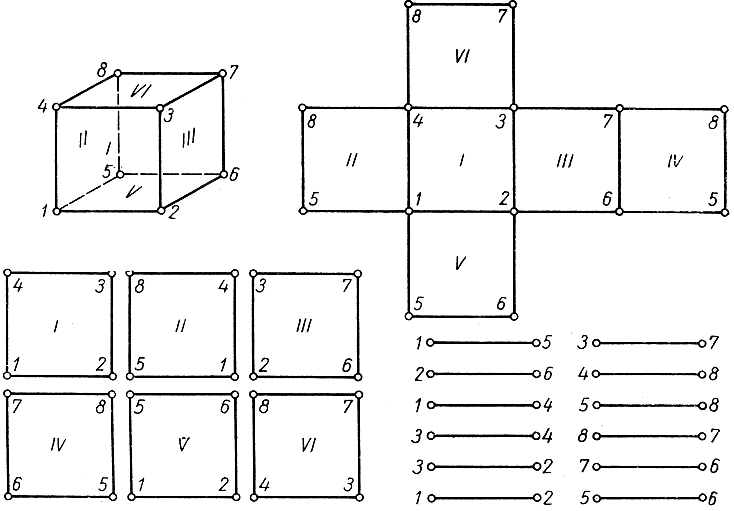
Рис. 117. Определение куба по сопоставленным друг с другом вершинам и ребрам

Вообще, любой многогранник в трехмерном пространстве R₃ приводится таким образом или к системе плоских многоугольников, или к системе прямолинейных отрезков.

Упражнение. Выполнить указанную редукцию для всех правильных многогранников (см. стр. 269).

Теперь уже ясно, что мы можем обратить ход наших рассуждений, определяя многоугольник на плоскости с помощью системы прямолинейных отрезков и многогранник в пространстве R₃ с помощью системы многоугольников в R₂ или же при условии дальнейшей редукции с помощью опять-таки прямолинейных отрезков. Но тогда совершенно естественно определить "многогранник" в четырехмерном пространстве R₄ с помощью системы многогранников в R₃ при надлежащей идентификации двумерных граней; "многогранник" в R₅ - с помощью "многогранников" в R₄ и т. д. В конечном счете всякий "многогранник" в R_n сводится к системе отрезков.

Останавливаться на этом вопросе подробнее мы лишены возможности. Добавим лишь несколько замечаний, не приводя доказательств. "Куб" в R₄ ограничен 8 трехмерными кубами, из которых каждый имеет со своими "соседями" по идентифицированной двумерной грани. Такой куб имеет 16 вершин, в каждой вершине сходятся по четыре ребра; ребер всего имеется 32. В R₄ существует шесть правильных многогранников. Кроме "куба", имеется один многогранник, ограниченный 5 правильными тетраэдрами, один, ограниченный 16 тетраэдрами, один, ограниченный 24 октаэдрами, один, ограниченный 120 додекаэдрами, и еще один, ограниченный 600 тетраэдрами. Доказано, что в R_n при n>4 существует только 3 правильных многогранника: один с n+1 вершинами, ограниченный n+1 многогранниками из R_n-1, имеющими пои, (n-2)-мерных граней; один с 2ⁿ вершинами, ограниченный 2n многогранниками из R_n-1, имеющими по 2n-2 (n-2)-мерных граней; и еще один с 2n вершинами, ограниченный 2ⁿ многогранниками из R_n-1, имеющими по n(n-2)-мерных граней.

Упражнение. Сравнить определение "куба" из R₄, данное в пункте 2, с определением, данным в настоящем пункте, и установить, что прежнее "аналитическое? определение куба равносильно настоящему "комбинаторному".

Со структурной, или "комбинаторной", точки зрения простейшими геометрическими фигурами размерности 0, 1, 2, 3 являются соответственно точка, отрезок, треугольник, тетраэдр. Ради единообразия символики обозначим фигуры этого типа соответственно Т₀, T₁, Т₂, Т₃. (Значки указывают на размерность.) Структура каждой из этих фигур характеризуется тем, что каждая фигура типа Т_n имеет n+1 вершин и каждое подмножество из i+1 вершин фигуры типа T_n (i = 0, 1, ..., n) определяет некоторую фигуру типа Т_i. Например, трехмерный тетраэдр Т₃ имеет 4 вершины, 6 ребер и 4 грани.

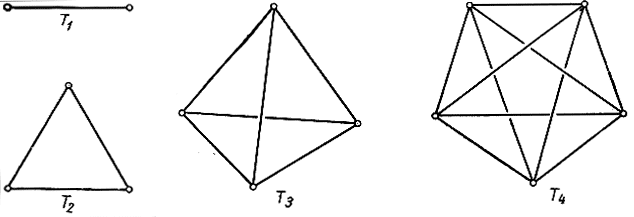
Рис. 118. Простейшие элементы в 1, 2, 3, 4 измерениях

Ясно, как будет дальше. Мы определим четырехмерный "тетраэдр" T₄ как множество, состоящее из 5 вершин, причем каждое подмножество из 4 вершин порождает фигуру типа T₃, каждое подмножество из 3 вершин - фигуру типа Т₂ и т. д. Фигура типа Т₄ схематически показана на рис. 118; мы видим, что у нее 5 вершин, 10 ребер, 10 треугольных граней и 5 тетраэдров.

Обобщение на n измерений не представляет труда. Из теории соединении известно, что существует ровно 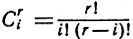таких различных подмножеств по i объектов, которые могут быть составлены из множества r объектов. Поэтому n-мерный "тетраэдр" содержит

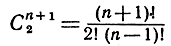ребер (фигур типа T₁),

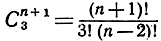треугольников (фигур типа T₂),

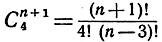фигур типа Т₃,

Упражнение. Нарисовать схематически фигуру типа Т₅ и определить число фигур типа T_i, в ней содержащихся (i = 0, 1, ..., 5).