2. Аналитический подход

Мы уже имели случай обратить внимание читателя на изменение роли аналитической геометрии, происшедшее на протяжении ее развития. Точки, прямые, кривые линии и т. д. первоначально рассматривались как чисто геометрические объекты, и задачей аналитической геометрии было всего-навсего, сопоставляя им координаты или уравнения, интерпретировать и развивать дальше геометрическую теорию алгебраическими или аналитическими методами. Но с течением времени постепенно начала утверждаться противоположная точка зрения. Число х, или пара чисел х, y, или тройка чисел х, y, z стали рассматриваться как исходные, основные объекты, и эти аналитические объекты, далее, конкретизировались, или, еще лучше сказать, "визуализировались" в виде точек на прямой, на плоскости, в пространстве. Теперь геометрический язык стал служить для того, чтобы констатировать наличие тех или иных отношений между числами. При этом мы лишаем геометрические объекты их самостоятельного и независимого значения и говорим, что пара чисел х, y есть точка на плоскости, совокупность всех пар х, y, удовлетворяющих линейному уравнению L (х, y) = ах + by + с = 0 (где а, b, с - данные постоянные числа), есть прямая линия и т. д. Такие же определения устанавливаются и для трехмерного пространства.

Даже в том случае, когда мы занимаемся собственно алгебраической проблемой, язык геометрии нередко представляется вполне удобным для краткого и совершенно точного описания фактов, и геометрическая интуиция начинает работать, подсказывая правильные алгебраические процедуры. Например, решая систему трех линейных уравнений с тремя неизвестными х, y, z

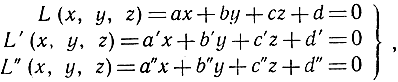
мы истолковываем стоящую перед нами задачу геометрически и говорим, что в трехмерном пространстве R₃ требуется найти точку пересечения трех плоскостей, заданных уравнениями L = 0, L' = 0, L" = 0. Другой пример: рассматривая все такие числовые пары х, y, что х>0, мы скажем, что имеем дело с полуплоскостью, расположенной вправо от оси y. В более общем случае совокупность числовых пар х, y, для которых выполняется неравенство

интерпретируется как полуплоскость, лежащая по одну сторону прямой L = 0, а совокупность таких числовых троек х, y, z, что

- как "полупространство", определяемое плоскостью L = 0.

После этих разъяснений нам совсем легко перейти к "четырехмерному" или даже к "n-мерному" пространству. Рассмотрим четверку чисел х, y, z, t. Скажем, что такая четверка представляет собой точку, или, еще проще, есть точка в четырехмерном пространстве R₄. Вообще, по определению, точка n-мерного пространства R_n есть не что иное, как система из n действительных чисел х₁, х₂, ... х_n, записанных в определенном порядке. Не так важно, что мы не "видим" этой точки. Геометрический язык не перестает быть вполне понятным в случае, если идет речь об алгебраических свойствах n переменных. Дело в том, что многие алгебраические свойства линейных уравнений и т. п. совершенно не зависят от числа входящих переменных, или, как принято говорить, от размерности пространства этих переменных. Мы назовем, таким образом, "гиперплоскостью" совокупность всех таких точек х₁, х₂, ..., х_n в n-мерном пространстве R_n, которые удовлетворяют линейному уравнению

Точно так же основная алгебраическая задача решения системы п линейных уравнений с п неизвестными

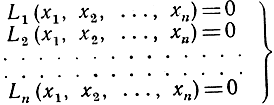
истолковывается на геометрическом языке как нахождение точки пересечения n гиперплоскостей L₁ = 0, L₂ = 0, ..., L_n = 0.

Преимущество такого геометрического способа описания математических фактов заключается в том, что он подчеркивает некоторые обстоятельства алгебраического характера, которые не зависят от числа измерений n и вместе с тем в случае n≤ могут быть наглядно интерпретированы. Во многих приложениях употребление геометрической терминологии имеет также преимущество краткости, а вместе с тем облегчает аналитические рассуждения, а иногда руководит ими и направляет их в должную сторону. Теория относительности снова может быть приведена здесь в качестве примера области, в которой существенный успех был достигнут по той причине, что три пространственные координаты х, y, z и временная координата t "события" были объединены в одно "пространственно-временное" четырехмерное многообразие х, y, z, t. Подчиняя, таким образом, "пространство - время" этой аналитической схеме и наделяя его, кроме того, свойствами неевклидовой геометрии, удалось описать многие весьма сложные ситуации с замечательной простотой. Столь же полезными оказались n-мерные пространства в механике, в статистической физике, не говоря уже о самой математике.

Приведем еще кое-какие чисто математические примеры. Совокупность всех кругов на плоскости образует трехмерное многообразие, так как круг с центром х, y и радиусом t может быть изображен точкой с координатами х, y, t. Так как радиус круга есть положительное число, то совокупность рассматриваемых точек заполняет полупространство. Таким же образом совокупность всех сфер в обыкновенном трехмерном пространстве образует четырехмерное многообразие, так как каждая сфера с центром х, y, z и радиусом t может быть представлена точкой с координатами х, y, z, t. Куб в трехмерном пространстве с центром в начале координат, ребрами длины 2 и гранями, параллельными координатным плоскостям, состоит из совокупности всех точек х₁, х₂, х₃, для которых |x₁|≤1, |x₂|≤1|x₃|≤1. Так же точно "куб" в n-мерном пространстве R_n с центром в начале координат, "ребрами" длины 2 и "гранями", параллельными координатным плоскостям, определяется как совокупность точек х₁, х₂, ..., х_n, для которых одновременно справедливы неравенства |x₁|≤1, |x₂|≤1, ..., |x_n|≤1. "Поверхность" такого куба состоит из всех точек, для которых хотя бы в одном из этих соотношений имеет место знак равенства. Поверхностные элементы размерности n-2 состоят из точек, для которых знак равенства стоит по меньшей мере два раза, и т. д.

Упражнение. Дайте описание поверхности такого куба в трехмерном, четырехмерном, n-мерном пространствах.