5. Эллиптическая, или риманова, геометрия

В евклидовой геометрии, как и в гиперболической геометрии Бойаи - Лобачевского, молчаливо допускается, что всякая прямая бесконечна (бесконечность прямой существенно связана с отношением "быть между" и аксиомами порядка). Но после того как гиперболическая геометрия открыла путь к свободному построению геометрий, естественно возник вопрос о том, нельзя ли осуществить построение таких неевклидовых геометрий, в которых прямые линии конечны и замкнуты. Разумеется, в таких геометриях теряют силу не только постулат о параллельных, но и аксиомы порядка. Современные исследования выяснили значение этих геометрий для новейших физических теорий. Впервые такие геометрии были подвергнуты рассмотрению в речи, произнесенной в 1851 г. Риманом при вступлении его в должность приват-доцента Гёттингенского университета. Геометрии с замкнутыми конечными прямыми могут быть построены без каких бы то ни было противоречий Вообразим двумерный мир, состоящий из поверхности S сферы, причем под "прямыми" условимся понимать большие круги сферы. Это был бы самый естественный способ описывать "мир" мореплавателя: дуги больших кругов являются кратчайшими кривыми, связывающими две точки на сфере, а это как раз и есть характеристическое свойство прямых на плоскости. В рассматриваемом двумерном мире всякие две "прямые" пересекаются, так что из внешней точки нельзя провести ни одной "прямой", не пересекающейся с данной (т. е. ей параллельной). Геометрия "прямых" в этом мире называется эллиптической геометрией. Расстояние между двумя точками в такой геометрии измеряется просто как длина кратчайшей дуги большого круга, проходящего через данные точки. Углы измеряются так же, как и в евклидовой геометрии. Самым характерным свойством эллиптической геометрии мы считаем несуществование параллельных.

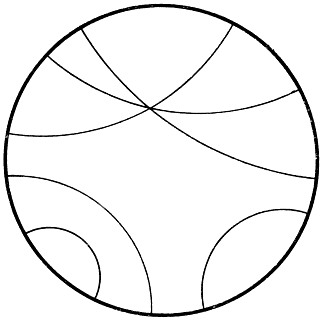
Рис. 112. Модель неевклидовой плоскости Пуанкаре

Следуя Риману, мы можем обобщить эту геометрию следующим образом. Рассмотрим "мир", состоящий из некоторой кривой поверхности в пространстве (не обязательно сферы) и определим "прямую линию", проходящую через две точки, как кратчайшую кривую ("геодезическую"), соединяющую эти точки. Точки поверхности можно разбить на два класса: 1°. Точки, в окрестности которых поверхность подобна сфере в том отношении, что она вся лежит по одну сторону от касательной плоскости в этой точке. 2°. Точки, в окрестности которых поверхность седлообразна (лежит по обе стороны касательной плоскости). Точки первого класса называются эллиптическими точками поверхности - по той причине, что при небольшом параллельном перемещении касательной плоскости она пересечет поверхность по кривой, имеющей вид эллипса; точки же второго класса носят название гиперболических, так как при аналогичном перемещении касательной плоскости получается пересечение с поверхностью, напоминающее гиперболу. Геометрия геодезических "прямых" в окрестности точки поверхности является эллиптической или гиперболической, смотря по тому, будет ли сама точка эллиптической или гиперболической. На этой модели неевклидовой геометрии углы измеряются, как в обыкновенной евклидовой геометрии.

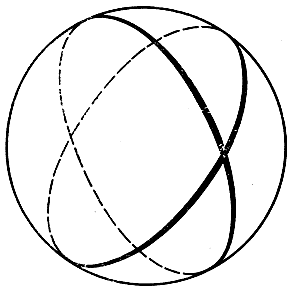
Рис. 113. 'Прямые линии' в геометрии Римана

Изложенная идея была развита Риманом дальше: он рассмотрел геометрии пространства, аналогичные только что разобранным геометриям поверхности. По Риману, "кривизна" пространства, меняясь от точки к точке, определяет характер геометрии в окрестности точки. "Прямые линии" у Римана - геодезические кривые. В эйнштейновой общей теории относительности геометрия пространства есть риманова геометрия; свет распространяется по геодезическим линиям, а кривизна пространства в каждой точке определяется в зависимости от свойств материи в окрестности точки.

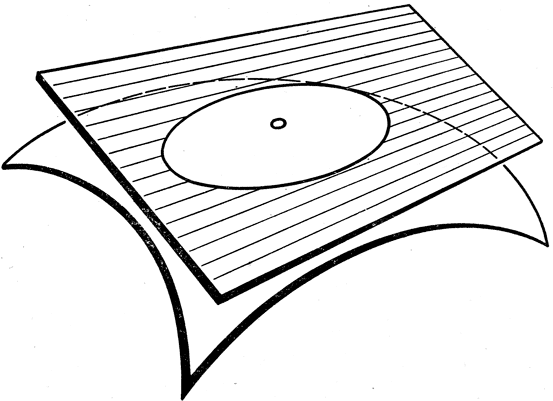
Рис. 114. Эллиптическая точка

Возникнув из чисто аксиоматических изысканий, неевклидова геометрия в наши дни стала чрезвычайно полезным аппаратом, допускающим различные применения при изучении физической реальности. В теории относительности, в оптике, в общей теории колебаний неевклидово описание явлений оказывается в ряде случаев гораздо более адекватным физической реальности, чем евклидово.

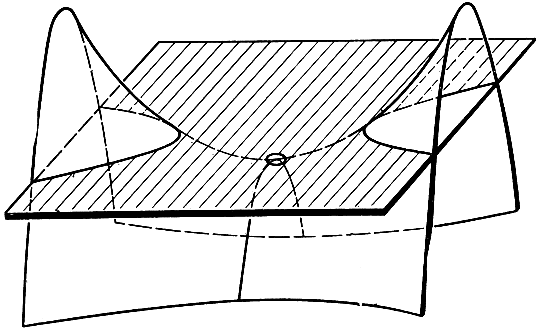
Рис. 115. Гиперболическая точка