2. Гиперболическая неевклидова геометрия

В системе Евклида имеется одна аксиома, относительно которой - на основе сопоставления с эмпирическими данными, с привлечением туго натянутых нитей или световых лучей - никак нельзя сказать, является ли она "истинной". Это знаменитый постулат о параллельных, утверждающий, что через данную точку, расположенную вне данной прямой, можно провести одну и только одну прямую, параллельную данной. Своеобразной особенностью этой аксиомы является то, что содержащееся в ней утверждение касается свойств прямой на всем ее протяжении, причем прямая предполагается неограниченно продолженной в обе стороны: сказать, что две прямые параллельны,- значит утверждать, что у них нельзя обнаружить общей точки, как бы далеко их ни продолжать. Вполне очевидно, что в пределах некоторой ограниченной части плоскости, как бы эта часть ни была обширна, напротив, можно провести через данную точку множество прямых, не пересекающихся с данной прямой. Так как максимально возможная длина линейки, нити, даже светового луча, прослеживаемого с помощью телескопа, непременно конечна и так как внутри круга конечного радиуса существует много прямых, проходящих через данную точку и в пределах круга не встречающихся с данной прямой, то отсюда следует, что постулат Евклида никогда не может быть проверен экспериментально. Все прочие аксиомы Евклида имеют конечный характер, т. е. касаются конечных отрезков прямых или конечных частей рассматриваемых плоских фигур. Тот факт, что аксиома параллельности не допускает эмпирической проверки, выдвигает на первый план вопрос о том, является ли она независимой от прочих аксиом. Если бы она была неизбежным логическим следствием других аксиом, то тогда нужно было бы просто вычеркнуть ее из списка аксиом и доказывать как теорему с помощью иных евклидовых аксиом. Много столетий математики пытались найти такое доказательство; этому способствовало широко распространенное среди всех, кто занимался геометрией, смутное сознание того, что аксиома параллельности по своему характеру существенно отличается от остальных, что ей недостает той убеждающей наглядности, которой, казалось бы, должно было обладать всякое геометрическое предложение, возводимое в ранг аксиомы.

Одна из первых попыток в указанном направлении была сделана в IV столетии н. э. комментатором Евклида Проклом, который, чтобы избежать необходимости вводить специальный постулат о параллельных прямых, ввел определение, согласно которому прямая, параллельная данной прямой, есть геометрическое место точек, расположенных от нее на одном и том же заданном расстоянии. При этом Прокл упустил из виду, что таким образом трудность не устраняется, а только перемещается, так как при его ходе мыслей остается недоказанным, что названное геометрическое место действительно есть прямая линия. Так как последнего Прокл доказать не мог, то именно это предложение .ему пришлось бы принять в качестве аксиомы параллельности, и ничто не было бы выиграно, так как мы можем легко установить, что обе упомянутые аксиомы эквивалентны между собой. Саккери (1667-1733), а затем Ламберт (1728-1777) делали попытки доказать аксиому параллельности косвенным путем, допуская противоположное утверждение и выводя из него абсурдные следствия. Но выведенные ими следствия оказались далеко не абсурдными: это были теоремы неевклидовой геометрии, получившей позднее дальнейшее развитие. Если бы названные лица рассматривали свои результаты не как нелепости, а как утверждения, свободные от внутренних противоречий, то не кому иному, как им, принадлежала бы заслуга открытия неевклидовой геометрии.

Но в те времена любую геометрическую систему, не находящуюся в абсолютном согласии с евклидовой, непременно стали бы рассматривать как очевидную нелепость. Кант, наиболее влиятельный философ той эпохи, выразил свое отношение к вопросу, утверждая, что аксиомы Евклида - не что иное, как неизбежные формы человеческого мышления, чем, по его мнению, и объясняется их объективная значимость по отношению к "реальному" пространству. Эта вера в аксиомы Евклида, как в незыблемые истины, существующие в сфере чистой интуиции, была одним из главных догматов кантовской философии. Однако с течением времени ни укоренившиеся навыки мышления, ни влияние философских авторитетов не смогли подавить растущего убеждения, что неизменные неудачи в поисках доказательства аксиомы параллельности имели своей причиной не столько недостаток изобретательности со стороны геометров, сколько тот основной факт, что этот постулат на самом деле независим от других. (Подобным же образом неудачи в решении при помощи радикалов общего уравнения пятой степени мало-помалу привели к подозрению, позднее оправдавшемуся, что такое решение невозможно.) Венгерский математик Бойаи (1802-1860) и русский математик Лобачевский (1793-1856) положили конец сомнениям, построивши во всех деталях геометрическую систему, в которой аксиома параллельности была отвергнута. Когда молодой гениальный энтузиаст Бойаи послал свою работу "королю математики" Гауссу, от которого с нетерпением ждал поддержки, то получил в ответ уведомление, что самим Гауссом открытие было сделано раньше, но он воздержался в свое время от публикации результатов, опасаясь слишком шумных обсуждений.

Посмотрим, что же означает независимость аксиомы параллельности. Эту независимость следует понимать в том смысле, что возможно свободное от внутренних противоречий построение "геометрических" предложений о точках, прямых и т. д., исходя из системы аксиом, в которой аксиома параллельности заменена противоположной. Такое построение называется неевклидовой геометрией. Нужно было интеллектуальное бесстрашие Гаусса, Бойаи и Лобачевского, чтобы осознать, что геометрия, основанная не на евклидовой системе аксиом, может быть абсолютно непротиворечивой.

Чтобы убедиться в непротиворечивости новой геометрии, нет надобности развивать во всех подробностях многочисленные теоремы неевклидовой геометрии, как это делали Бойаи и Лобачевский. Мы умеем теперь строить простые "модели" такой геометрии, удовлетворяющие всем аксиомам Евклида, кроме аксиомы параллельности. Простейшая модель была указана Феликсом Клейном, на работы которого в этой области оказали влияние идеи английского геометра Кэли (1821-1895). В такой модели через данную точку, лежащую вне данной прямой, можно провести бесчисленное множество "прямых", "параллельных" данной прямой. Подобного рода геометрия называется геометрией Бойаи - Лобачевского, или "гиперболической" геометрией. (Основание для последнего наименования будет приведено на стр. 258-259.)

При построении модели Клейна сначала рассматриваются объекты обыкновенной евклидовой геометрии; и затем некоторые из этих объектов и отношений между ними переименовываются таким образом, что для их описания оказывается пригодной уже неевклидова геометрия. Эта последняя тем самым не в меньшей мере непротиворечива, чем первоначальная евклидова геометрия, так как излагается (если посмотреть с другой точки зрения и описывать другими словами) как совокупность фактов обыкновенной евклидовой геометрии. С этой моделью можно легко освоиться, привлекая кое-какие понятия из проективной геометрии.

При проективном преобразовании одной плоскости на другую или на саму себя (можно после отображения совместить обе плоскости) окружность, вообще говоря, переходит в некоторое коническое сечение. Но можно легко показать (доказательства мы не приводим), что существует бесчисленное множество таких проективных преобразований плоскости на саму себя, при которых данный круг (вместе со всеми внутренними точками) переходит сам в себя. При таких преобразованиях внутренние точки, как и точки контура, меняют, вообще говоря, свои места, но внутренние точки остаются внутренними, а точки контура остаются на контуре. (Центр круга, как легко убедиться, можно перевести в любую наперед заданную внутреннюю точку.) Рассмотрим совокупность всех таких преобразований. Конечно, они не будут оставлять очертания фигур неизменными и потому не являются движениями в обычном смысле. Но мы теперь сделаем решающий шаг и назовем их "неевклидовыми движениями" в той геометрии, которую строим. Посредством этих "движений" можно дальше определить и "равенство": две фигуры называются равными, если существует "неевклидово движение", переводящее одну фигуру в другую.

Перейдем теперь к описанию упомянутой выше клейновой модели гиперболической геометрии. "Плоскость" состоит только из внутренних точек круга, внешние точки просто отбрасываются. Каждая внутренняя точка называется неевклидовой "точкой", каждая хорда круга называется неевклидовой "прямой"; "движения" и "равенства" уже определены выше; проведение "прямой" через две "точки" и нахождение "точки" пересечения двух "прямых" совершаются, как в евклидовой геометрии. Легко убедиться, что новая конструкция удовлетворяет всем постулатам евклидовой геометрии с единственным исключением - постулатом о параллельных прямых. Что этот постулат здесь не выполняется, видно ясно из того, что через "точку", не лежащую на "прямой", можно провести бесчисленное множество "прямых", не имеющих общей "точки" с данной прямой. Данная "прямая" есть евклидова хорда, тогда как в качестве второй "прямой" может быть взята любая из хорд, проходящих через данную "точку" и не пересекающих первой "прямой" внутри круга. Описанная простая модель совершенно достаточна для того, чтобы покончить с основным вопросом, породившим неевклидову геометрию: она показывает, что аксиома параллельности не выводится из остальных аксиом евклидовой геометрии. Действительно, если бы она выводилась из них, то тогда была бы верной теоремой и по отношению к модели Клейна, а мы видим, что это не так.

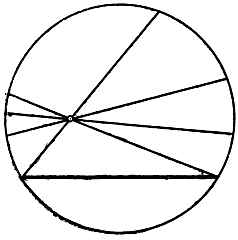
Рис. 110. Модель неевклидовой плоскости Клейна

Строго говоря, предыдущая аргументация построена на допущении, что модель Клейна непротиворечива, т. е. что нельзя доказать вместе с некоторым утверждением также и противоположного утверждения. Но, во всяком случае, геометрия модели Клейна непротиворечива в такой же степени, как и обыкновенная евклидова геометрия, так как теоремы о "точках" и "прямых" и т. д. модели Клейна представляют собой только своеобразно сформулированные теоремы евклидовой геометрии. Удовлетворительного доказательства непротиворечивости аксиом евклидовой геометрии дано не было, если не считать сведения к аналитической геометрии и в конечном счете к числовому континууму; а непротиворечивость концепции континуума - также вопрос открытый^*.

^* (Подробнее об исследованиях в этой области см. упомянутую на стр. 116 книгу А. Френкеля и И. Бар-Хиллела, содержащую также обширную библиографию.)

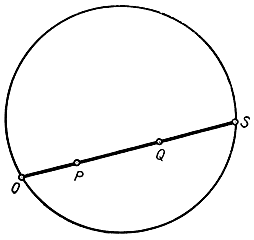
Рис. 111. Неевклидово расстояние

* Мы привлечем внимание читателя еще к одной детали (впрочем, стоящей за пределами непосредственно поставленных нами задач), именно к определению неевклидова "расстояния" в модели Клейна. Это "расстояние" должно быть инвариантно относительно неевклидовых "движений", так как обыкновенное движение не изменяет обыкновенного расстояния. Мы знаем, что двойное отношение есть инвариант проективного преобразования. Естественно возникает мысль о том, чтобы при определении "расстояния" между двумя различными точками Р и Q внутри нашего круга воспользоваться двойным отношением (OSQP), тле О и S- точки, в которых продолженный в обе стороны отрезок РQ встречается с окружностью. Это двойное отношение, в самом деле, есть положительное число, но взять это отношение непосредственно в качестве "расстояния" PQ не представляется удобным. Действительно, в предположении, что три точки Р, Q, R лежат на одной прямой, мы должны были бы иметь равенство 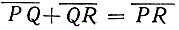, но, вообще говоря,

Напротив, справедливо несколько иное равенство

в самом деле,

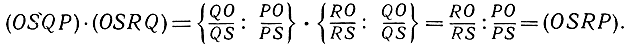
Свойство (1) позволяет определить "расстояние" РQ как логарифм двойного отношения (а не как само двойное отношение), с таким расчетом, чтобы обеспечить аддитивность расстояния: Это "расстояние" есть положительное число, так как при P≠Q (OSQP)>1.

1. Из основного свойства логарифма (см. стр. 479) следует, в силу (1), что 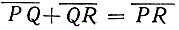. По какому основанию брать логарифмы - несущественно, так как при изменении основания меняется лишь единица измерения. Между прочим, если одна из точек, скажем Q, приближается к окружности, то неевклидово расстояние РQ неограниченно возрастает. Это означает, что "прямая" нашей неевклидовой модели имеет бесконечную неевклидову "длину", хотя в евклидовом смысле представляет собой конечный отрезок.