5. Гиперболоид

В трехмерном пространстве мы встречаемся с так называемыми квадриками (поверхностями второго порядка), которые в данном случае играют ту же роль, что конические сечения (кривые второго порядка) на плоскости.

Простейшими из них являются сфера и эллипсоид. Квадрики более разнообразны, чем конические сечения, и изучение их связано с большими трудностями. Мы рассмотрим бегло и без доказательств одну из самых интересных поверхностей этого типа: так называемый связный (или однополостный) гиперболоид.

Эта поверхность может быть получена следующим образом. Возьмем в пространстве три прямые l₁, l₂, l₃, находящиеся в общем положении. Последнее означает, что никакие две из них не параллельны и все три не являются параллельными одной и той же плоскости. Может показаться удивительным, что существует бесконечное множество прямых в пространстве, из которых каждая пересекается со всеми тремя данными прямыми. Убедимся в этом. Пусть π - произвольная плоскость, содержащая прямую l₁; эта плоскость пересекает прямые l₂ и l₃ в двух точках, и прямая m, проведенная через эти две точки, очевидно, пересекается со всеми прямыми l₁, l₂ и l₃. Когда плоскостью вращается около прямой l₁, прямая m будет изменять свое положение, однако все время продолжая пересекаться с тремя данными прямыми. При движении m возникает поверхность, неограниченно уходящая в бесконечность, которая и называется однополостным гиперболоидом. Она содержит бесконечное множество прямых типа m. Любые три такие прямые, скажем m₁, m₂ и m₃, также будут находиться в общем положении, и те прямые в пространстве, которые будут пересекаться с тремя прямыми m₁, m₂ и m₃ одновременно, также будут лежать на рассматриваемой поверхности. Отсюда следует основное свойство гиперболоида: он составляется из двух различных семейств прямых линий; каждые три линии одного и того же семейства находятся в общем положении и каждая прямая одного семейства пересекается со всеми прямыми другого.

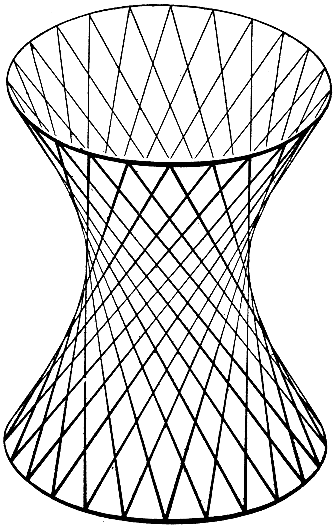
Рис. 109. Гиперболоид

Важное проективное свойство гиперболоида заключается в том, что двойное отношение тех четырех точек, в которых данная четверка прямых одного семейства пересекается с некоторой прямой второго семейства, не зависит от выбора этой последней. Это утверждение вытекает из метода построения гиперболоида с помощью вращающейся плоскости, и читатель может убедиться в его справедливости в качестве упражнения.

Отметим еще одно замечательное свойство гиперболоида: хотя он содержит два семейства прямых линий, но существование этих прямых не препятствует изгибанию поверхности- не делает ее жесткой. Если устроить модель гиперболоида из стержней, способных свободно вращаться около точек взаимных пересечений, то поверхность в целом может быть непрерывно деформируема, пробегая бесконечное множество различных состояний.