4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений

Одной из лучших иллюстраций принципа двойственности применительно к коническим сечениям является взаимоотношение между общими теоремами Паскаля и Брианшона. Первая из них была открыта в 1640 г., вторая - в 1806 г. И, однако, каждая из них есть непосредственное следствие другой, так как всякая теорема, формулировка которой упоминает только конические сечения, прямые и точки, непременно остается справедливой при изменении формулировки по принципу двойственности.

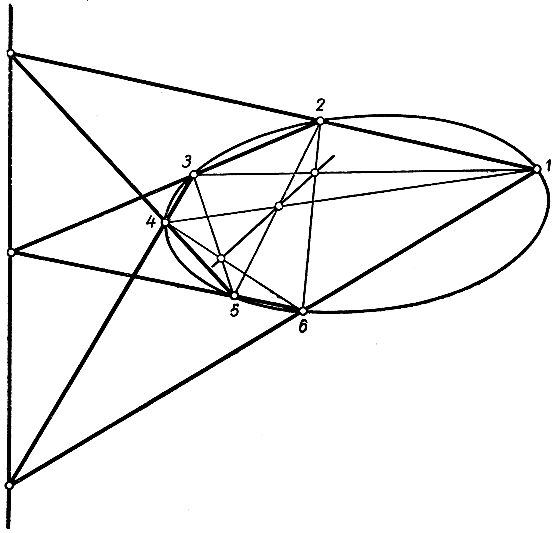
Рис. 105. Общая конфигурация Паскаля. Показаны два случая: один для шестиугольника 1, 2, 3, 4, 5, 6, другой для шестиугольника 1, 3, 5, 2, 6, 4

Теоремы, доказанные в § 5 под теми же наименованиями, представляют собой "случаи вырождения" следующих более общих теорем.

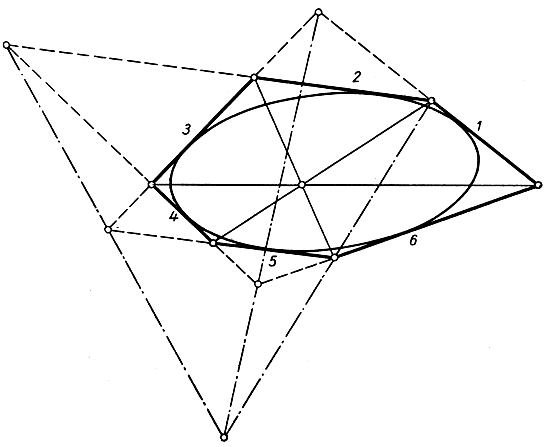
Рис. 106. Общая конфигурация Брианшона. Показаны только два случая

Теорема Паскаля. Противоположные стороны шестиугольника, вписанного в коническое сечение, пересекаются в трех коллинеарных точках.

Теорема Брианшона. Три диагонали, соединяющие противоположные вершины шестиугольника, описанного около конического сечения, конкуррентны.

Обе теоремы имеют, очевидно, проективное содержание. Их двойственность бросается в глаза, если сформулировать их следующим образом:

Теорема Паскаля. Дано шесть точек 1, 2, 3, 4, 5, 6 на коническом сечении. Соединим последовательные точки прямыми (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 1). Отметим точки пересечения прямых (1 ,2) и (4, 5), (2, 3) и (5,6), (3,4 )и (6,1). Эти три точки лежат на одной прямой.

Теорема Брианшона. Дано шесть касательных 1, 2, 3,4, 5, 6 к коническому сечению. Последовательные касательные пересекаются в точках (1,2), (2,3), (3,4), (4,5), (5,6), (6,1). Проведем прямые, соединяющие точки (1, 2) и (4,5), (2,3) и (5,6), (3,4) и (6,1). Эти три прямые проходят через одну точку.

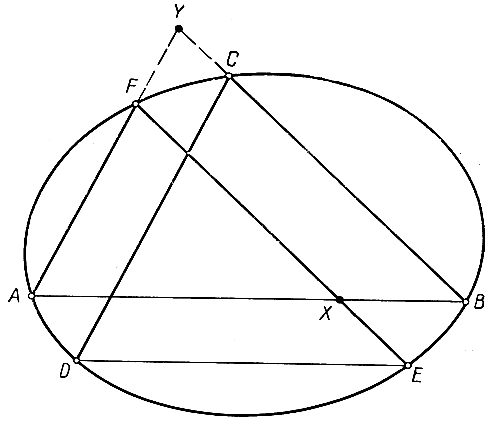
Рис. 107. Доказательство теоремы Паскаля

Доказательства проводятся с помощью специализации такого же рода, как и в рассмотренных раньше случаях вырождения. Докажем теорему Паскаля. Пусть A, В, С, D, Е, F - вершины шестиугольника, вписанного в коническое сечение К Посредством проектирования можно сделать параллельными прямые AB и ED, FA и CD (и тогда получится конфигурация, изображенная на рис. 107; ради удобства шестиугольник на чертеже взят самопересекающимся, хотя в этом нет никакой необходимости). Нам нужно теперь доказать только-одно, что прямая СВ параллельна прямой FE, другими словами, что противоположные стороны пересекаются на бесконечно удаленной прямой. Для доказательства рассмотрим четверку точек F, A, в, D, которая, как мы знаем, при проектировании из любой точки К сохраняет одно и то же двойное отношение, скажем, k. Станем проектировать из точки С на прямую AF; получим четверку точек F, A, Y, ∞, причем

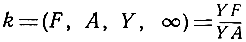
(см. стр. 216).

Станем теперь проектировать из точки Е на прямую ВА; получим четверку точек X, A, В, ∞, причем

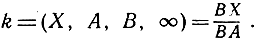
Итак,

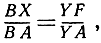
что как раз и обозначает, что YB||FX. Доказательство теоремы Паскаля закончено.

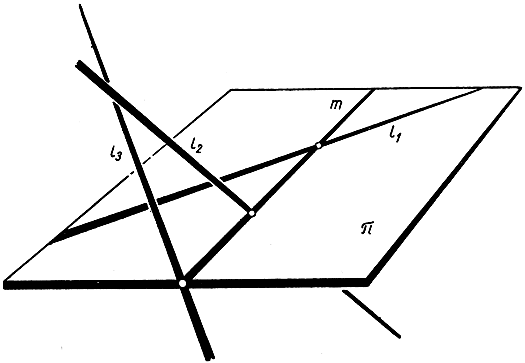
Рис. 108. Построение прямых, пересекающих три данные прямые общего положения

Теорема Брианшона, как было указано, следует из теоремы Паскаля по принципу двойственности. Но ее можно доказать и непосредственно - путем рассуждения, двойственного относительно только что приведенного. Провести это рассуждение во всех деталях будет прекрасным упражнением для читателя.