3. Конические сечения как "линейчатые кривые"

Понятие касательной к коническому сечению принадлежит проективной геометрии, так как касательная к коническому сечению есть прямая, имеющая с самой кривой только одну общую точку, а это - свойство, сохраняющееся при проектировании. Проективные свойства касательных к коническим сечениям основываются на следующей теореме: Двойное отношение точек пересечения четырех фиксированных касательных к коническому сечению с произвольной пятой касательной не зависит от выбора этой пятой касательной.

Доказательство этой теоремы весьма просто. Так как любое коническое сечение есть проекция окружности и так как в теореме идет речь только о таких свойствах, которые инвариантны относительно проектирования, то,чтобы доказать теорему в общем случае, достаточно доказать ее для частного случая окружности.

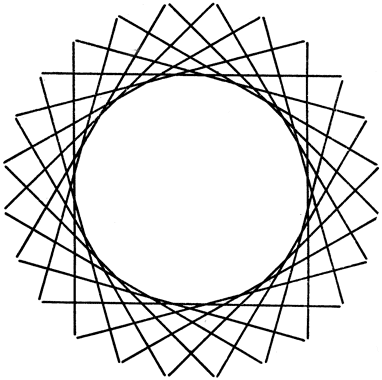
Рис. 100. Окружность как совокупность касательных

Для этого же частного случая теорема доказывается средствами элементарной геометрии. Пусть Р, Q, R, S - четыре точки на окружности К; а, b, с, d - касательные в этих точках; Т - еще какая-нибудь точка на окружности; о - касательная в этой точке; пусть, далее, А, В, С, D - точки пересечения касательной о с касательными а, b, с, d. Если М - центр окружности, то, очевидно, ∧ ТМА = ∧ ТМР, и последнее выражение представляет угол, вписанный в K, опирающийся на дугу ТР. Таким же образом ∧ ТМВ представляет угол, вписанный в K и опирающийся на дугу TQ. Следовательно,

∧ AMB = ¹/₂ PQ,

где ¹/₂PQ обозначает угол, вписанный в К и опирающийся на дугу PQ. Отсюда видно, что А, В, С, D проектируются из М четырьмя прямыми, углы между которыми имеют величины, зависящие только от положения точек Р, Q, R, S. Но тогда двойное отношение (ABCD) зависит только от четырех касательных а, b, с, d, но не от касательной о. Как раз это и нужно было установить.

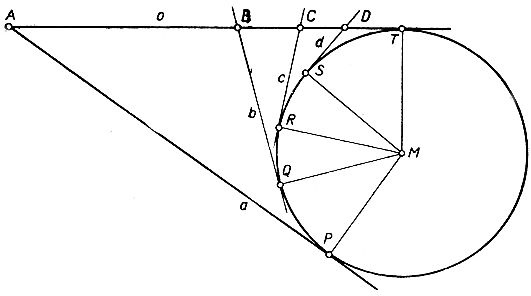
Рис. 101. Свойство касательной к окружности

В предыдущем пункте мы имели случай убедиться, что коническое сечение может быть построено "по точкам", если станем отмечать точки пересечения взаимно соответствующих прямых двух пучков, между которыми установлено проективное соответствие. Только что доказанная теорема дает нам возможность сформулировать двойственную теорему. Возьмем две касательные а и а' к коническому сечению К. Третья касательная t пусть пересекает а и а' соответственно в точках А и А'. Если t будет перемещаться вдоль кривой, то установится соответствие

между точками а и точками а'. Это соответствие будет проективным, так как по доказанной теореме произвольная четверка точек на а будет непременно иметь тоже двойное отношение, что и соответствующая четверка точек на а'. Отсюда следует, что коническое сечение К, рассматриваемое как "совокупность своих касательных", "состоит" из прямых, соединяющих взаимно соответствующие точки двух точечных рядов^* на а и на а', находящихся в проективном соответствии. Указанное обстоятельство позволяет ввести новое определение конических сечений, рассматриваемых на этот раз как "линейчатые кривые". Сравним это определение с прежним проективным определением конического сечения, данным в предыдущем пункте:

Коническое сечение, рассматриваемое как совокупность точек, состоит из точек пересечения взаимно соответствующих прямых в двух проективных пучках.

Коническое сечение, рассматриваемое как "совокупность прямых, состоит из прямых, соединяющих взаимно соответствующие точки в двух проективных рядах.

^* (Совокупность точек на прямой называется точечным рядом. Это понятие двойственно по отношению к понятию пучка прямых.)

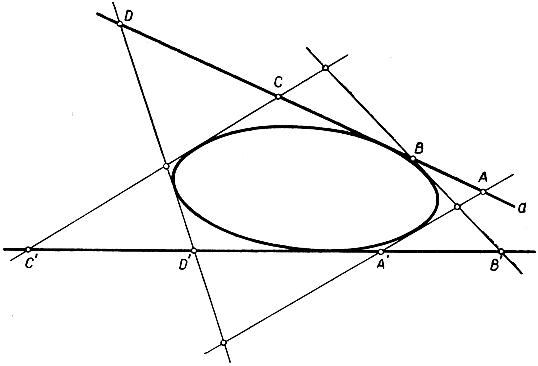
Рис. 102. Проективные ряды точек на двух касательных к эллипсу

Если мы станем считать касательную к коническому сечению в некоторой его точке двойственным элементом по отношению к самой точке и условимся, кроме того, "линейчатую кривую" (образованную совокупностью касательных) на основе двойственности сопоставлять "точечной кривой" (образованной совокупностью точек), то предыдущие формулировки будут безупречны с точки зрения принципа двойственности. При "переводе" одной формулировки в другую с заменой всех понятий соответствующими двойственными понятиями "коническое сечение" остается неизменным: но в одном случае оно мыслится как "точечная кривая", определяемая своими точками, в другом - как "линейчатая кривая", определяемая своими касательными.

Из предыдущего вытекает важное следствие: принцип двойственности, первоначально установленный в проективной геометрии плоскости только для точек и прямых, оказывается, может быть распространен и на конические сечения. Если в формулировке любой теоремы, касающейся точек, прямых и конических сечений, заменить каждый элемент ему двойственным (не упуская из виду, что точке конического сечения должна быть сопоставляема касательная к этому коническому сечению), то в результате также получится справедливая теорема. Пример действия этого принципа мы встретим в пункте 4 настоящего параграфа.

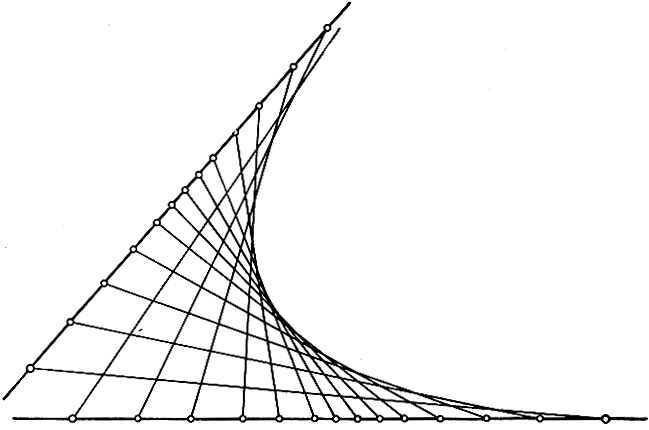
Рис. 103. Парабола, определенная конгруэнтными точечными рядами

Построение конических сечений, понимаемых как "линейчатые кривые", показано на рис. 103-104. В частности, если в двух проективных точечных рядах бесконечно удаленные точки соответствуют взаимно одна другой (так будет непременно, если точечные ряды конгруэнтны или подобны^*), то коническое сечение будет параболой; справедливо и обратное утверждение.

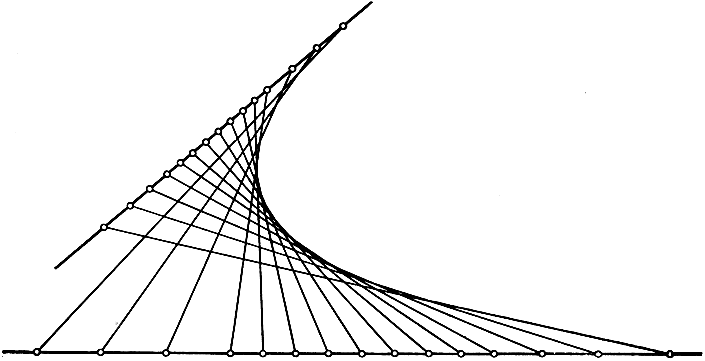
Рис. 104. Парабола, определенная подобными точечными рядами

^* (Что такое "конгруэнтные" и "подобные" точечные ряды, достаточно понятно без объяснений.)

Упражнение. Доказать обратную теорему: на двух неподвижных касательных к параболе движущаяся касательная к параболе определяет два подобных точечных ряда.