2. Проективные свойства конических сечений

Основываясь на положениях, установленных в предыдущем пункте, примем теперь временно следующее определение: коническое сечение есть проекция окружности на плоскость. Это определение в большей степени отвечает духу проективной геометрии, чем общепринятые фокальные определения, так как эти последние всецело опираются на метрическое понятие расстояния. Новое определение тоже не вполне свободно от этого недостатка, поскольку "окружность" - также метрическое понятие. Но через мгновение мы придем к чисто проективному определению конических сечений.

Раз мы приняли, что коническое сечение есть не что иное, как проекция окружности (другими словами, под термином "коническое сечение" мы понимаем любую кривую, принадлежащую проективному классу окружности; см. стр. 217), то отсюда сейчас же следует, что всякое свойство окружности, инвариантное относительно проективных преобразований, должно также принадлежать любому коническому сечению. Вспомним теперь следующее хорошо известное - метрическое - свойство окружности: "Вписанные в окружность углы, опирающиеся на одну и ту же дугу, равны между собой". На рис. 96 угол АОВ, опирающийся на дугу АВ, не зависит от положения точки О на окружности. Свяжем, дальше, указанное обстоятельство с проективным понятием двойного отношения, вводя на окружности уже не две точки A, В, а четыре: А, B, С, D. Четыре прямые а, b, с, d, соединяющие эти точки с точкой О на окружности, имеют двойное отношение (а, b, с, d), зависящее только от углов, опирающихся на дуги СА, СВ, DA, DB. Соединяя А, В, С, D с какой-нибудь другой точкой О' на окружности, получим прямые а', b', c', d'. Из отмеченного ранее свойства окружности вытекает, что две четверки прямых "конгруэнтны"^*. Поэтому у них будет одно и то же двойное отношение: (a'b'c'd') = (abcd). Спроектируем окружность на некоторое коническое сечение К: тогда на К получится четверка точек, которые мы снова обозначим через A, В, С, D, две точки О и О' и две четверки прямых а, b, с, d и а', b', с', d'. Эти две четверки прямых уже не будут конгруэнтны, так как углы при проектировании, вообще говоря, не сохраняются. Но так как двойное отношение при проектировании не изменяется, то равенство (abcd) = (a'b'c'd') по-прежнему имеет место. Мы пришли, таким образом, к следующей основной теореме: Если четыре точки конического сечения К, например А, В, С, D, соединены с пятой точкой О того же сечения прямыми a, b, с, d, то двойное отношение (abcd) не зависит от положения О на кривой К (рис. 97).

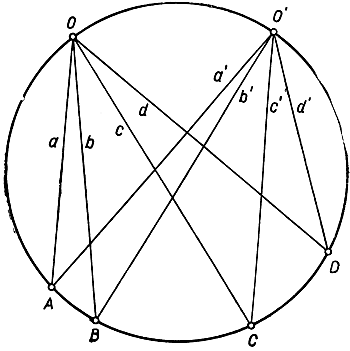
Рис. 96. Двойное отношение на окружности

^* (Четверка прямых а, b, с, d считается конгруэнтной другой четверке а', b', с', d', если углы между каждой парой прямых в первой четверке равны как по величине, так и по направлению отсчета углам между соответствующими прямыми второй четверки.)

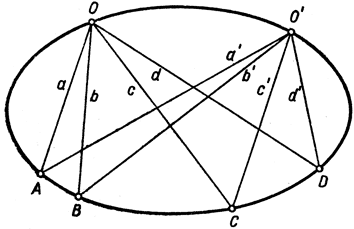
Рис. 97. Двойное отношение на эллипсе

Это - замечательный результат. Как нам уже известно, если четыре точки А, В, С, D взяты на прямой, то двойное отношение, составленное из соединяющих эти точки с пятой точкой О прямых, не зависит от выбора этой пятой точки. Это - исходное положение, лежащее в основе проективной геометрии. Теперь мы узнали, что аналогичное утверждение справедливо и относительно четырех точек, взятых на некотором коническом сечении K, однако с существенным ограничением: пятая точка О уже не может свободно двигаться по всей плоскости, а может только перемещаться по коническому сечению К.

Не представляет особого труда доказать и обратную теорему в следующей форме: Если на кривой К имеются две точки О и О', обладающие тем свойством, что, какова бы ни была четверка точек А, В, С, D на кривой K, двойные отношения, составленные из прямых, соединяющих эти точки с О, и из прямых, соединяющих эти точки с О', равны между собой, то кривая К есть коническое сечение (а уж тогда, по прямой теореме, двойное отношение, составленное из прямых, соединяющих четыре данные точки с произвольной точкой О" на K, будет иметь одно и то же постоянное значение). Но доказательства мы здесь приводить не будем.

Изложенные проективные свойства конических сечений наводят на мысль об общем методе точечного построения этих кривых. Условимся под пучком прямых понимать совокупность всех прямых плоскости, проходящих через данную точку О. Рассмотрим пучки прямых, проходящих через две точки О и О', расположенные на коническом сечении K. Между прямыми пучка О и прямыми пучка О' можно установить взаимно однозначное соответствие, сопоставляя прямой а из первого пучка прямую а' из второго всякий раз, как а и а' встречаются в некоторой точке А кривой K. Тогда любая четверка прямых а, b, с, d из пучка О будет иметь то же двойное отношение, что и соответствующая четверка а', b', с', d' из пучка О'. Всякое взаимно однозначное соответствие между двумя пучками прямых, обладающее этим последним свойством, называется проективным соответствием. (Это определение двойственно по отношению к определению проективного соответствия между точками на двух прямых, см. стр. 208-209.) Пользуясь этим определением, можно теперь утверждать: Коническое сечение К есть геометрическое место точек пересечения взаимно соответствующих прямых из двух пучков, находящихся в проективном соответствии. Полученная теорема подводит фундамент под следующее чисто проективное определение конических сечений: Коническим сечением называется геометрическое место точек пересечения взаимно соответствующих прямых из двух пучков, находящихся в проективном соответствии^*. Как ни соблазнительно проникнуть в глубь теории конических сечений, строящейся на таком определении, мы вынуждены ограничиться лишь немногими замечаниями по этому поводу.

^* (Это геометрическое место при известных обстоятельствах может вырождаться в прямую; см. рис. 98.)

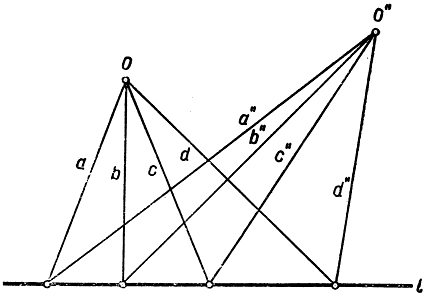
Рис. 98. К построению проективных пучков прямых

Пары пучков, находящихся в проективном соответствии, можно получить следующим образом. Спроектируем все точки Р прямой линии l из двух разных центров О и О" и установим между проектирующими пучками взаимно однозначное соответствие, сопоставляя друг другу те прямые, которые пересекаются на прямой l. Этого достаточно, чтобы полученные пучки находились в проективном соответствии. Затем возьмем пучок О" и перенесем его "как нечто твердое" в произвольное положение O'. Что новый пучок О' будет находиться в проективном соответствии с пучком О, это совершенно очевидно. Но замечательно то, что любое проективное соответствие между двумя пучками можно получить именно таким образом. (Это положение двойственно по отношению к утверждению из упражнения 1 на стр. 209.) Если пучки О и О' конгруэнтны, получается окружность. Если углы между соответствующими лучами в двух пучках равны, но отсчитываются в противоположных направлениях, то получается равносторонняя гипербола (рис. 99).

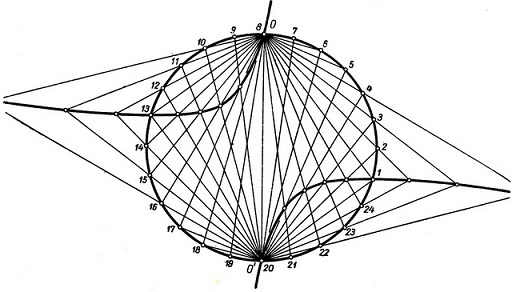
Рис. 99. Образование окружности и равносторонней гиперболы с помощью проективных пучков

Следует еще заметить, что указанное определение конического сечения может, в частности, дать и прямую линию, как это показано на рис. 98. В этом случае прямая 00" соответствует сама себе и все ее точки должны быть рассматриваемы как принадлежащие искомому геометрическому месту. Таким образом, коническое сечение вырождается в пару прямых: это обстоятельство вполне согласуется с тем фактом, что существуют сечения конуса, состоящие из двух прямых (если секущая плоскость проходит через вершину конуса).

Упражнения.

1. Вычертить эллипсы, гиперболы и параболы с помощью проективных пучков. (Читателю настойчиво рекомендуется экспериментировать с подобного рода построениями. Это в высшей степени способствует пониманию сути дела.)
2. Дано пять точек О, О', А, В, С некоторого конического сечения K. Найти точки пересечения D произвольной прямой d пучка О с кривой К. (Указание. Проведите через О прямые ОА, ОВ, ОС и назовите их а, b, с. Через О' проведите прямые ОА, О'В, О'С и назовите их а', b', с'. Проведите через О прямую d и постройте такую прямую d' пучка О', что (abcd) = (a'b'c'd'). Тогда точка пересечения d и d' принадлежит кривой K.)