§ 8. Конические сечения и квадрики

1. Элементарная метрическая геометрия конических сечений

До сих пор мы занимались только точками, прямыми, плоскостями и фигурами, составленными из конечного числа этих элементов. Если бы проективная геометрия ограничивалась рассмотрением таких "линейных" фигур, она была бы сравнительно малоинтересна. Но фактом первостепенного значения является то обстоятельство, что проективная геометрия этим не ограничивается, а включает также обширную область конических сечений и их многомерных обобщений. Аполлониева метрическая трактовка конических сечений - эллипсов, гипербол и парабол - была одним из выдающихся успехов античной математики. Едва ли можно переоценить значение конических сечений как для чистой, так и для прикладной математики (например, орбиты планет и орбиты электронов в атоме водорода являются коническими сечениями). Не приходится удивляться тому, что классическая, возникшая в древней Греции теория конических сечений и в наши дни составляет необходимую часть математического образования. Но греческая геометрия никоим образом не сказала последнего слова. Через две тысячи лет были открыты замечательные проективные свойства конических сечений. Несмотря на простоту и изящество этих свойств, академическая инерция до настоящего времени служит препятствием их проникновению в школьное преподавание.

Начнем с того, что напомним метрические определения конических сечений. Таких определений несколько, и их эквивалентность доказывается в элементарной геометрии. Наиболее распространенные определения связаны с фокусами кривых. Эллипс определяется как геометрическое место таких точек Р на плоскости, что сумма их расстояний r₁ и r₂ от двух данных точек F₁ и F₂, называемых фокусами, имеет постоянное значение. (Если фокусы совпадают, кривая превращается в окружность.) Гипербола определяется как геометрическое место таких точек Р на плоскости, что абсолютное значение разности r₁ - r₂ равно одной и той же постоянной величине. Парабола определяется как геометрическое место точек Р, расстояние которых r от данной точки F равно расстоянию от данной прямой l.

В аналитической геометрии эти кривые представляются уравнениями второй степени относительно прямоугольных координат х, y. Нетрудно доказать, обратно, что всякая кривая, представляемая уравнением второго порядка

есть или одно из трех названных выше конических сечений, или прямая линия, или пара прямых, или сводится к одной точке, или носит чисто мнимый характер. Как показывается во всяком курсе аналитической геометрии, для доказательства достаточно сделать надлежащим образом подобранную замену координатной системы.

Указанные выше определения конических сечений - существенно метрические: в них используется понятие расстояния. Но вот другое определение, устанавливающее место конических сечений в проективной геометрии: конические сечения суть не что иное, как проекции окружности на плоскость. Если мы станем проектировать окружность С из некоторой точки О, то проектирующие прямые образуют бесконечный двойной конус, и пересечение этого конуса с плоскостью π будет проекцией окружности С. Кривая пересечения будет эллипсом или гиперболой, смотря по тому, пересечет ли плоскость только одну "полость" конуса или обе. Возможен и промежуточный случай параболы, если плоскость я параллельна одной из проектирующих прямых, проведенных через О (рис. 94).

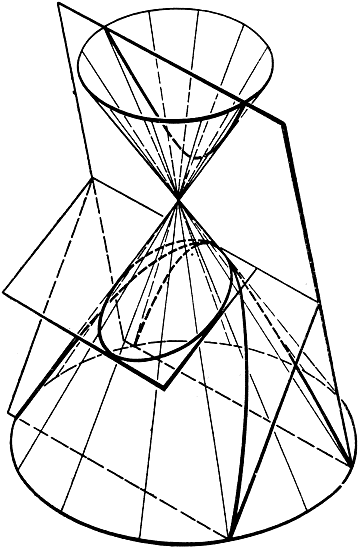
Рис. 94. Конические сечения

Проектирующий конус не обязан быть "прямым круговым" с вершиной О, расположенной вертикально над центром круга С: он может быть и "наклонным". Но во всех случаях (как мы примем здесь, не приводя доказательства) в пересечении конуса с плоскостью получается кривая, уравнение которой - второй степени; и обратно, всякая кривая второго порядка может быть получена из окружности посредством проектирования. По этой именно причине кривые второго порядка иначе называются коническими сечениями.

Мы уже отметили, что если плоскость пересекает только одну "полость" прямого кругового конуса, то пересечение Е представляет собой эллипс. Нетрудно установить, что кривая Е удовлетворяет обыкновенному фокальному определению эллипса, которое было сформулировано выше. Приведем очень простое и изящное доказательство, данное в 1822 г. бельгийским математиком Данделеном. Представим себе две сферы S₁ и S₂ (рис. 95), которые касаются плоскости сечения π соответственно в точках F₁ и F₂ и, кроме того, касаются конуса вдоль параллельных окружностей К₁ и K₂. Взяв произвольную точку Р кривой Е, проведем отрезки PF₁ и PF₂. Затем рассмотрим отрезок РО, соединяющий точку Р с вершиной конуса О; этот отрезок целиком лежит на поверхности конуса; обозначим через Q₁ и Q₂ точки его пересечения с окружностями К₁ и К₂. Так как PF₁ и РQ₁ - две касательные, проведенные из точки Р к одной и той же сфере S₁, то

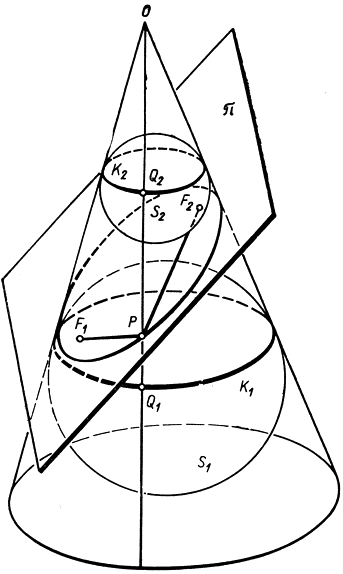
Рис. 95. Сферы Данделена

Точно так же

Складывая эти равенства, мы получаем:

Но PQ₁ + PQ₂ = Q₁Q₂ есть расстояние между параллельными окружностями К₁ и К₂ на поверхности конуса: оно не зависит от выбора точки Р на кривой Е. Отсюда следует, что, какова бы ни была точка Р на E, имеет место равенство

а это и есть фокальное определение эллипса. Итак, Е есть эллипс, а F₁ и F₂ - его фокусы.

Упражнение. Если плоскость пересекает обе "полости" конуса, то кривая пересечения - гипербола. Доказать это утверждение, помещая по одной сфере в каждой из "полостей" конуса.