*2. Однородные координаты. Алгебраические основы двойственности

В обыкновенной аналитической геометрии прямоугольными координатами точки на плоскости являются снабженные знаками расстояния точки от двух взаимно перпендикулярных осей. Но в такой системе координат не находится места для бесконечно удаленных точек расширенной проективной плоскости. Поэтому если мы хотим пользоваться аналитическими методами в проективной геометрии, то необходимо найти такую координатную систему, которая смогла бы включить идеальные точки наравне с обыкновенными. Легче всего дать описание такой координатной системы, если представить себе данную плоскость X, Y (которую будем обозначать через π), расположенной в трехмерном пространстве с прямоугольными координатами х, y, z (эти буквы обозначают снабженные знаками расстояния точки от трех координатных плоскостей, образованных осями х,уиг). Представим себе, что плоскость я параллельна координатной плоскости х, y и находится на расстоянии 1 от нее, так что трехмерные координаты точки Р в плоскости π будут (X, Y, 1). Принимая начало О координатной системы за центр проектирования, заметим, что всякой точке Р взаимно однозначно соответствует некоторая прямая ОР, проходящая через начало координат (см. стр. 105). В частности, бесконечно удаленным точкам плоскости π соответствуют прямые, проходящие через О и параллельные π.

Посмотрим теперь, что же представляет собой система однородных координат для точек плоскости π. Чтобы найти однородные координаты обыкновенной точки Р в этой плоскости, возьмем прямую ОР и на ней выберем произвольную точку Q, отличную от О (рис. 93). Обыкновенные трехмерные координаты х, y, z точки Q считаются однородными координатами точки Р в плоскости π. В частности, координаты (X, Y, 1) самой точки Р являются ее однородными координатами. Но вместе с тем ее же однородными координатами явятся любые числа (tX, tY, t), где t ≠0, так как координаты всех точек прямой ОР (кроме О) имеют как раз такой вид. (Мы исключаем точку (0, 0, 0), потому что она лежит на всех прямых, проходящих через О, и не может служить для их различения.)

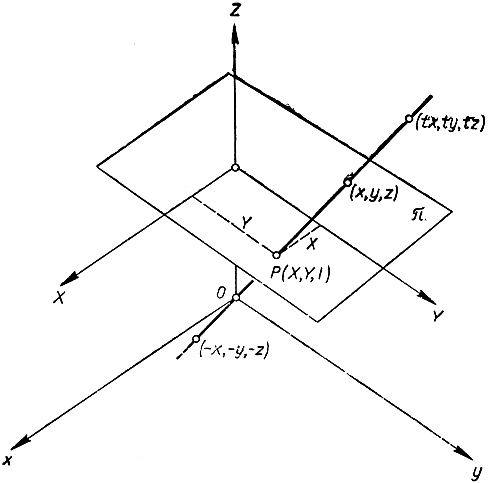
Рис. 93. Однородные координаты

Система однородных координат, конечно, представляет известное неудобство в том отношении, что нужны три числа вместо двух для определения точки, и, самое главное, координаты точки определяются не однозначно, а с точностью до постоянного множителя. Но она имеет то безусловное преимущество, что охватывает и идеальные, бесконечно удаленные точки плоскости я. Действительно, такой идеальной точке Р соответствует некоторая прямая, проходящая через О и параллельная π; всякая точка Q на такой прямой имеет координаты вида (х, y, 0); таким образом, однородные координаты идеальных точек плоскости π имеют вид (х, y, 0). Нетрудно написать в однородных координатах уравнение прямой линии на плоскости π. Для этого достаточно заметить, что прямые, соединяющие О с точками этой прямой, лежат в плоскости, проходящей через О. В аналитической геометрии доказывается, что уравнение такой плоскости имеет вид:

Это же есть и уравнение данной прямой в однородных координатах.

Теперь, когда геометрическая модель, изображающая точки плоскости я в виде прямых, проходящих через О, отслужила свою службу, можно ее отбросить и дать следующее, чисто аналитическое определение расширенной плоскости:

Точка есть не что иное, как тройка действительных чисел (х, y, z), из которых не все равны нулю. Две такие тройки (х₁, y₁, z₁) и (х₂, y₂, z₂) определяют одну и ту же точку, если существует такое число t≠0, что

Другими словами, можно, не меняя самой точки, умножать ее координаты на произвольный множитель, отличный от нуля. (Потому эти координаты и называются однородными.) Точка (х, y, z) обыкновенная, если z отлично от нуля, идеальная, если z равно нулю.

Прямая линия в плоскости π состоит из всех точек (х, y, z), удовлетворяющих линейному уравнению вида

где а, b, с - постоянные числа, не все равные нулю. В частности, бесконечно удаленные точки плоскости я удовлетворяют уравнению

согласно определению это также уравнение прямой, именно бесконечно удаленной прямой плоскости π. Так как прямая определяется уравнением вида (1'), то тройка чисел (а, b, с) может быть рассматриваема как однородные координаты прямой (1'). Далее следует, что при произвольном t≠0 тройка чисел (ta, tb, tc) представляет собой координаты той же прямой, так как уравнение

удовлетворяется в точности теми же координатными тройками (х, y, z), что и уравнение (1').

В этих определениях обнаруживается полная симметрия между точкой и прямой: и та и другая определяются тройкой чисел - однородными координатами (u, υ, ω). Условие того, что точка (х, y, z) лежит на прямой (a, b, c), выражается равенством

и это же есть вместе с тем условие того, что точка с координатами (а, b, с) лежит на прямой с координатами (х, y, z). Например, арифметическое тождество

означает, что точка (3, 4, 2) лежит на прямой (2, 1, -5) и в равной мере, что точка (2, 1, -5) лежит на прямой (3, 4, 2). Эта симметрия и представляет собой основу двойственности между точкой и прямой в проективной геометрии, так как всякое соотношение между точками и прямыми становится некоторым соотношением между прямыми и точками, если только координаты будут подвергнуты надлежащей переинтерпретации: координаты точек нужно при этом считать координатами прямых, координаты прямых - координатами точек. Все алгебраические операции и результаты остаются теми же самыми, но, толкуя их по-разному, мы получаем теорему, соответствующую первоначальной в смысле двойственности. Необходимо заметить, с другой стороны, что в обыкновенной плоскости X, Y ни о какой двойственности не может быть речи, так как уравнение прямой в обыкновенных координатах

несимметрично относительно X, Y и а, b, с. Только включение в рассмотрение бесконечно удаленных элементов (точек и прямой) обеспечивает применимость принципа двойственности.

Чтобы перейти от однородных координат х, у, z обыкновенной точки Р в плоскости π к обыкновенным прямоугольным координатам, мы просто полагаем 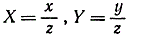. Тогда X, У обозначают расстояния точки Р от двух перпендикулярных осей в плоскости π, параллельной х- и y-осям, как показано на рис. 93. Мы знаем, что уравнение

представляет прямую в плоскости π. Полагая 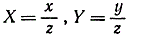и умножая на z, мы найдем, что уравнение той же прямой в однородных координатах будет

как это уже было указано на стр. 226. Так, уравнение прямой 2х - 3y + z = 0 в обыкновенных прямоугольных координатах X, Y примет вид 2Х - 3Y + 1 = 0. Разумеется, последнему уравнению бесконечно удаленная точка рассматриваемой прямой с однородными координатами (3, 2, 0) уже не отвечает.

Остается сказать еще одно. Нам удалось получить чисто аналитическое определение точки и прямой; но что можно сказать о важном понятии проективного преобразования? Можно установить, что проективное преобразование, понимаемое в том смысле, как это было разъяснено на стр. 208, задается аналитически системой линейных уравнений

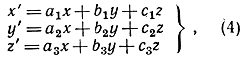
(4)

связывающих однородные координаты х', y', z' точек в плоскости π' с однородными координатами х, y, z точек в плоскости π. С аналогичной точки зрения можно определить проективное преобразование как такое, которое задается системой уравнений вида (4). Теоремы проективной геометрии тогда становятся теоремами, говорящими о поведении числовых троек (х, y, z) при таких преобразованиях. Например, доказательство инвариантности двойного отношения при проективных преобразованиях превращается в легкое упражнение из области алгебры линейных преобразований. Не будем вникать в детали этой аналитической процедуры и вернемся вместо того назад - к проективной геометрии в ее более наглядном аспекте.