§ 6. Аналитическое представление

1. Вводные замечания

В раннем периоде развития проективной геометрии существовала настойчиво проводимая тенденция выполнять все построения на синтетической, или, как говорилось, "чисто геометрической", основе, избегая вовсе применения чисел и алгебраических методов. Выполнение этой программы встретило на своем пути большие затруднения, так как всегда оставались какие-то пункты, в которых алгебраические формулировки казались неизбежными. Полный успех в построении чисто синтетической проективной геометрии был достигнут только к концу XIX в. и только ценой значительных осложнений. В этом отношении методы аналитической геометрии оказались гораздо более плодотворными. Для современной математики характерна иная тенденция - положить в основу построения понятие числа, и в геометрии эта тенденция, идущая от Ферма и Декарта, возымела решительный триумф. Аналитическая геометрия перестала быть подсобным аппаратом, играющим служебную роль в геометрических рассуждениях, и стала самостоятельной областью, в которой интуитивная геометрическая интерпретация операций и результатов уже не является последней и окончательной целью, а принимает на себя функцию руководящего принципа, помогающего угадывать и понимать аналитические факты. Такое изменение значения геометрии есть последствие постепенного развития геометрии в историческом плане- развития, широко раздвинувшего рамки классических концепций; оно же обусловило вместе с тем почти органическое слияние геометрии и анализа.

В аналитической геометрии под "координатами" геометрического объекта понимается какая угодно совокупность чисел, позволяющая определить, этот объект однозначно. Так, точка определяется своими прямоугольными координатами х, y или своими полярными координатами ρ, θ; с другой стороны, например, треугольник определяется координатами трех вершин, что в целом составляет шесть координат. Мы знаем, что прямая линия в плоскости х, y представляет собой геометрическое место всех точек Р (x, y) (об обозначениях см. стр. 99), координаты которых удовлетворяют некоторому линейному уравнению

Поэтому можно три числа а, b, с назвать "координатами" этой прямой. Например, а = 0, b = 1, c = 0 определяют прямую y = 0, т. е. ось x; a = 1, b = -1, с = 0 определяют прямую х = y, которая делит пополам угол между положительным направлением оси х и положительным направлением оси y. Таким же образом следующие уравнения определяют "конические сечения": х² + y² = r² - окружность радиуса r с центром в начале координат, (х - а)² + (y - b)² = r² - окружность радиуса r с центром (а, b),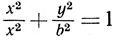 - эллипс и т. д.

Более или менее наивный подход к аналитической геометрии заключается в том, чтобы, отправляясь от чисто "геометрических" представлений - точка, прямая и т. д.,- переводить их затем на язык чисел. Современная точка зрения противоположна. Мы отправляемся от множества всевозможных пар чисел х, y и называем каждую такую пару точкой, так как можем, если пожелаем, наглядно интерпретировать такую пару чисел с помощью общедоступного понятия геометрической точки. Точно так же прямая линия является геометрическим представлением или интерпретацией линейного уравнения, связывающего х и y. Указанный перенос акцента от интуитивного понимания геометрии к аналитическому открывает возможность, в частности, простой и вполне строгой трактовки бесконечно удаленных точек в проективной геометрии; он же необходим для более глубокого проникновения в эту область. Для тех читателей, которые обладают достаточной предварительной математической подготовкой, мы дадим теперь некоторый очерк применения аналитических методов в проективной геометрии.