4. Теорема Брианшона

Эта теорема формулируется так: Если стороны шестиугольника проходят поочередно через две данные точки Р и Q, то три диагонали, соединяющие противоположные вершины шестиугольника, конкуррентны (рис. 91).

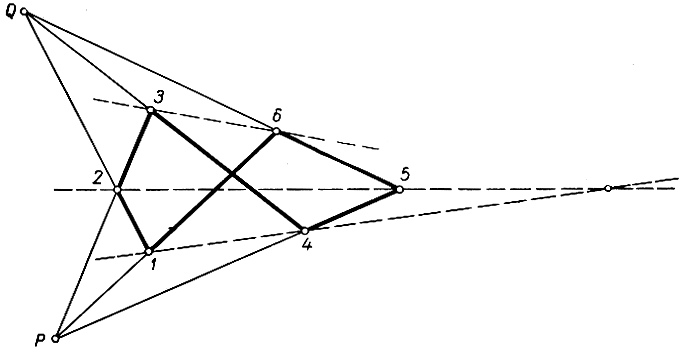
Рис. 91. Конфигурация Брианшона

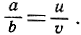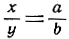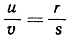Посредством предварительного проектирования можно отправить в бесконечность точку Р и точку, в которой пересекаются две какие-нибудь диагонали, например 14 и 36. Полученная ситуация изображена на рис. 92. Так как 14||36, то Но вместе с тем и Значит, 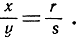и поэтому 36||25, так что все три диагонали параллельны и, следовательно, конкуррентны. Этого достаточно, чтобы считать теорему доказанной и в общем случае.

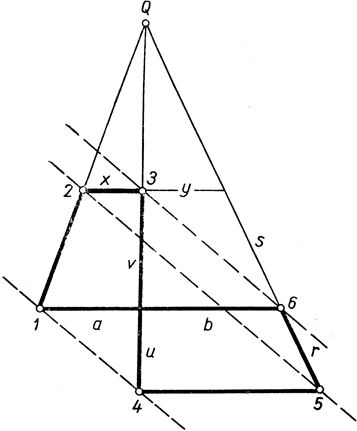
Рис. 92. Доказательство теоремы Брианшона