3. Теорема Паскаля

(Далее будет рассмотрена более общая теорема этого же типа. Настоящий частный случай связывается также с именем Паппа Александрийского (III столетие до нашей эры).)

Эта теорема формулируется так: Если вершины шестиугольника лежат поочередно на двух пересекающихся прямых, то точки Р, Q, R пересечения противоположных сторон этого шестиугольника коллинеарны (рис. 88). (Контур шестиугольника может быть самопересекающимся. Что такое "противоположные" стороны, легко понять из схемы на рис. 89.)

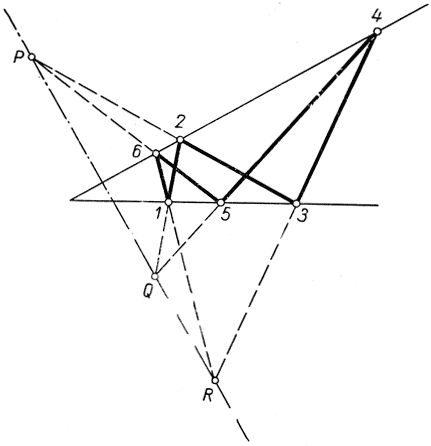
Рис. 88. Конфигурация Паскаля

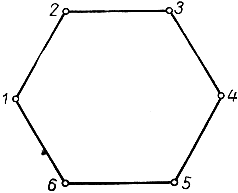
Рис. 89. Нумерация вершин шестиугольника

Выполняя предварительное проектирование, можно допустить, что Р и Q ушли в бесконечность. Остается показать, что R также уйдет в бесконечность. Ситуация иллюстрируется рис. 90, где 23||56 и 12||45. Нужно показать, что 16||34. Мы имеем:

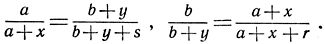
Поэтому

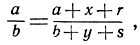
так что 16||34, что и требовалось доказать.

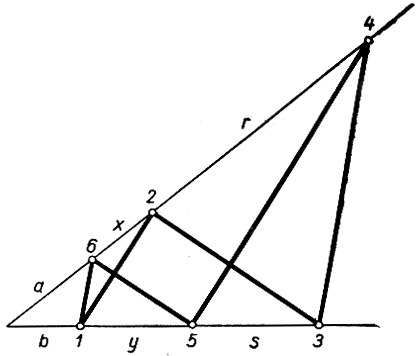
Рис. 90. Доказательство теоремы Паскаля