2. Двумерное доказательство теоремы Дезарга

Докажем теперь, не прибегая к пространственному проектированию, что если два треугольника АВС и А'В'С расположены на плоскости так, как изображено на рис. 72, т. е. если прямые, соединяющие соответствующие вершины, встречаются в одной и той же точке, то точки пересечения соответствующих сторон Р, Q, R лежат на одной прямой. Для этого прежде всего спроектируем чертеж таким образом, чтобы точки Q и R ушли в бесконечность. После такого проектирования прямая А'В' станет параллельна прямой AВ, а прямая А'С - прямой АС (рис. 87). Как было отмечено в пункте 1 настоящего параграфа, чтобы доказать теорему Дезарга в общем случае, достаточно доказать ее только для случая рассматриваемой здесь частной конфигурации. Именно достаточно показать, что точка Р пересечения сторон ВС и В'С также уйдет в бесконечность, т. е. что прямая В'С параллельна прямой ВС: тогда точки Р, Q, R будут коллинеарны (так как все три будут лежать на бесконечно удаленной прямой). Обратим внимание на то, что

AB||A'B' влечет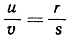

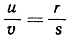
и

AС||A'С' влечет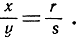

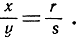
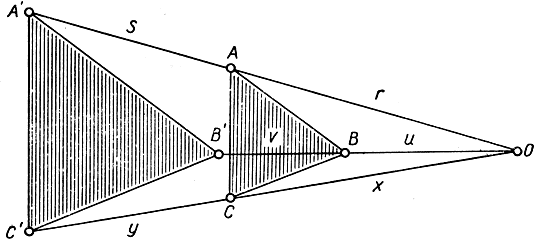
Рис. 87. Доказательство теоремы Дезарга

Поэтому 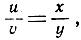а отсюда следует ВС||В'С', что и требовалось доказать.

Следует отметить, что приведенное доказательство теоремы Дезарга опирается на математическое понятие длины отрезка. Таким образом, проективная теорема доказана в данном случае метрическими средствами. Другое заслуживающее внимания обстоятельство заключается в следующем. Мы указывали раньше (стр. 209), что понятию проективного преобразования может быть дано "внутреннее" определение ("проективное преобразование плоскости - такое, которое оставляет инвариантными все двойные отношения"): отсюда вытекает, что теорема Дезарга способна быть сформулирована и доказана без выхода в пространство, т. е. без использования трехмерных представлений и построений.

Упражнение. Доказать подобным же образом теорему, обратную дезарговой: если треугольники ABC и А'В'С таковы, что Р, Q, R коллинеарны, то прямые АА', ВВ', СС' конкуррентны.