§ 5. Применения

1. Предварительные замечания

После введения бесконечно удаленных элементов уже нет необходимости явно оговаривать все исключительные случаи параллельности, возникающие при построениях и доказательствах теорем. Достаточно помнить, что если точка является бесконечно удаленной, то все проходящие через нее прямые параллельны. Отпадает и необходимость делать различие между центральной и параллельной проекциями, так как параллельная проекция есть не что иное, как проекция из бесконечно удаленной точки. На рис. 72 точка О или прямая PQR могут оказаться бесконечно удаленными (рис. 85 иллюстрирует первый из упомянутых случаев); мы предоставляем читателю в качестве упражнения сформулировать в "финитных" (т. е. не содержащих упоминания о бесконечности) терминах соответствующие утверждения дезарговой теоремы.

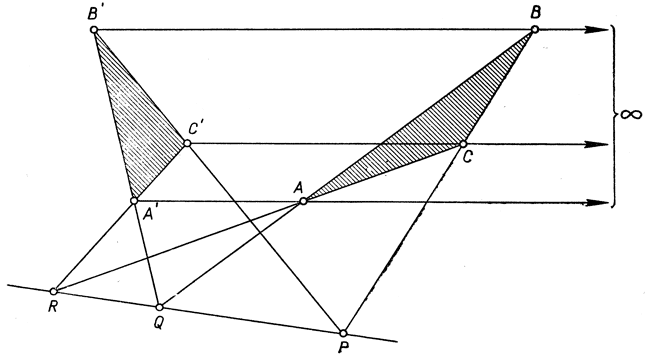
Рис. 85. Дезаргова конфигурация с центром в бесконечности

Не только формулировка, но и доказательство теоремы, принадлежащей проективной геометрии, нередко упрощаются в результате введения бесконечно удаленных элементов. Общий принцип заключается в следующем. Условимся под "проективным классом" некоторой геометрической фигуры F понимать класс всех фигур, в которые F может быть переведена проективными преобразованиями. Проективные свойства F ничем не отличаются от проективных свойств любой фигуры ее проективного класса, так как по самому определению проективные свойства сохраняются при проектировании. Таким образом, любая проективная теорема (т. е. теорема, говорящая только о проективных свойствах), которая верна для фигуры F, будет также верна для любого "представителя" проективного класса этой фигуры, и обратно. Поэтому, чтобы доказать такую теорему для F, достаточно доказать ее для некоторого "представителя" проективного класса F. Мы можем воспользоваться указанным обстоятельством и выбрать такого "представителя", для которого доказательство проще, чем для самой фигуры F. Например, произвольные две точки A, В плоскости π могут быть спроектированы в бесконечность из данного центра О, если проектировать на плоскость, параллельную плоскости, проходящей через точки О, A, В; прямые, проходящие через A или через В, при этом превратятся в семейства параллельных прямых. Именно такое предварительное преобразование мы выполним при доказательстве проективных теорем, которыми займемся в этом параграфе.

В дальнейшем нам придется воспользоваться следующим обстоятельством, относящимся к параллельным прямым. Пусть две прямые, проходящие через точку О, пересекаются прямыми l₁ и l₂ в точках A, В, C, D, как показано на рис. 86. Если прямые l₁ и l₂ параллельны, то 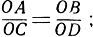и обратно, если выполнено последнее соотношение, то прямые l₁ и l₂ параллельны. Доказательство, вытекающее из элементарных свойств подобных треугольников, предоставляется читателю.

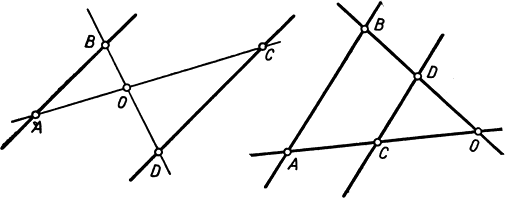
Рис. 86. Подобие треугольников, образованных параллельными прямыми