3. Двойное отношение с бесконечно удаленными элементами

Еще одно замечание следует сделать по поводу двойных отношений с бесконечно удаленными элементами. Будем обозначать символом ∞ бесконечно удаленную точку на прямой l. Посмотрим, как определяется символ (АВС ∞), если А, В, С - три обыкновенные точки на l. Пусть Р - некоторая точка на l; тогда (ABC) рассматривается как предел (АВСР), когда Р удаляется в бесконечность по l. Но

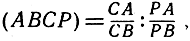
и, когда Р неограниченно удаляется, ^PA/_PB стремится к 1. Отсюда вытекает определение:

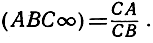
В частности, если (АВС∞) = 1, то С есть середина отрезка АВ: средняя точка отрезка и бесконечно удаленная точка, взятая в направлении отрезка, делят отрезок гармонически.

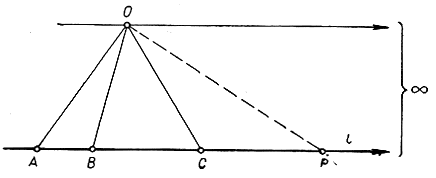
Рис. 84. Двойное отношение с участием бесконечно удаленной точки

Упражнение. Что представляет собой двойное отношение четырех прямых l₁, l₂, l₃, l₄, если они параллельны? Что получится, в частности, с этим двойным отношением, если в качестве l₄ будет взята бесконечно удаленная прямая?