2. Идеальные элементы и проектирование

Введение бесконечно удаленных точек и бесконечно удаленной прямой на плоскости позволит нам гораздо более удовлетворительным образом рассмотреть проектирование одной плоскости на другую. Пусть плоскость π проектируется на плоскость π' из центра О (рис. 83). Эта проекция устанавливает соответствие между точками и прямыми π и точками и прямыми π'. Каждой точке A на π соответствует единственная точка А' на π' со следующими исключениями: если выходящий из О проектирующий луч параллелен плоскости π', то он пересекает я в точке A, которой не соответствует никакая обыкновенная точка плоскости π'. Такие исключительные точки плоскости π расположены на прямой l, которой не соответствует никакая обыкновенная прямая плоскости π'. Но оговаривать эти исключения становится излишним, если мы условимся точке А сопоставлять бесконечно удаленную точку на плоскости π', взятую в направлении прямой ОA, а прямой l сопоставлять бесконечно удаленную прямую в плоскости π'. Аналогично некоторую бесконечно удаленную точку в плоскости π мы сопоставляем каждой точке В' на такой прямой m' в плоскости π', через которую проходят все лучи, выходящие из О и параллельные плоскости π. Самой прямой m соответствует бесконечно удаленная прямая плоскости π. Таким образом, посредством введения в плоскости бесконечно удаленных точек и прямой достигается то, что проекция одной плоскости, на другую устанавливает такое соответствие между точками и прямыми двух плоскостей, которое взаимно однозначно без всяких исключений. (Так устраняются исключения, упомянутые в сноске на стр. 203.) Далее, легко понять, что из принятых соглашений вытекает следствие: точка лежит на прямой, если проекция точки лежит на проекции прямой. Отсюда видно, что все теоремы, относящиеся к коллинеарным точкам, конкуррентным прямым и т. д. и говорящие только о точках, прямых и отношениях инцидентности, инвариантны относительно проектирования в расширенном смысле. Это дает возможность оперировать с бесконечно удаленными точками плоскости я, заменяя их соответствующими получающимися при проектировании обыкновенными точками плоскости π'.

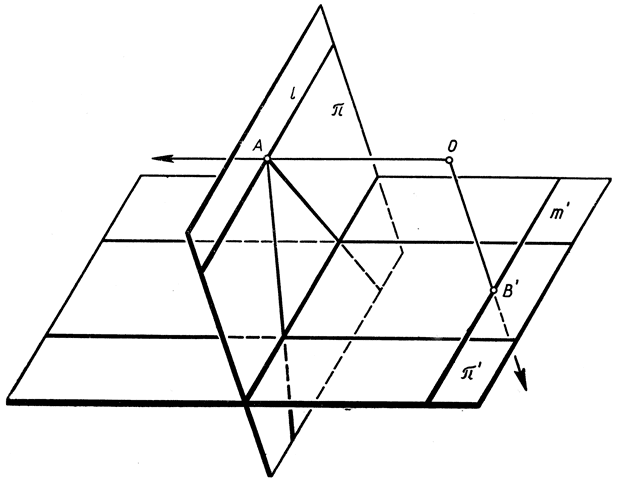
Рис. 83. Возникновение бесконечно удаленных элементов при проектировании

^* Можно воспользоваться интерпретацией бесконечно удаленных точек плоскости π с помощью проектирования из внешней точки О на обыкновенные точки .другой плоскости π', чтобы получить конкретную евклидову "модель" расширенной плоскости. Для этого не будем обращать внимания на плоскость π', а сосредоточимся на плоскости π и прямых, проходящих через О. Каждой обыкновенной точке π соответствует прямая, проходящая через О, непараллельная π; каждой бесконечно удаленной точке π - прямая, проходящая через О, параллельная π. Итак, совокупности всех точек π, обыкновенных и идеальных, соответствует совокупность прямых, проходящих через О, и это соответствие взаимно однозначно без всяких исключений. Точки на некоторой прямой в плоскости π переходят в прямые на плоскости, проходящей через О. Точка и прямая в плоскости я инцидентны в том и только в том случае, если инцидентны соответствующие прямая и плоскость, проходящие через О. Другими словами, геометрия инцидентности точек и прямых в расширенной плоскости совершенно равносильна геометрии инцидентности обыкновенных прямых и плоскостей, проходящих через фиксированную точку пространства.

Положение в трехмерном пространстве вполне аналогично, хотя отпадает возможность пользоваться наглядным аппаратом проектирования. Здесь тоже мы вводим особую бесконечно удаленную точку, связанную с каждым семейством параллельных прямых. В каждой плоскости имеется бесконечно удаленная прямая. Затем вводится новый элемент - бесконечно удаленная плоскость, состоящая из всех бесконечно удаленных точек пространства и содержащая все бесконечно удаленные прямые. С бесконечно удаленной плоскостью каждая обыкновенная плоскость пересекается по своей собственной бесконечно удаленной прямой.