2. Применение к полному четырехстороннику

В качестве интересного применения инвариантности двойного отношения мы докажем одну простую, но важную теорему проективной геометрии. Речь идет о полном четырехстороннике - фигуре, образованной произвольными четырьмя прямыми, из которых никакие три не являются конкуррентными, и шестью точками их пересечения. На рис. 81 названные четыре прямые суть AE, BE, ВI, AF. Прямые АВ, EG и IF являются диагоналями четырехсторонника. Рассмотрим одну из диагоналей, например AB, и отметим на ней точки С и D, где она пересекается с двумя другими диагоналями. Тогда теорема утверждает существование равенства (ABCD) = -1; словами это выражается так: точки пересечения одной диагонали с двумя другими делят отрезок между вершинами четырехсторонника гармонически. Для доказательства достаточно обратить внимание на то, что

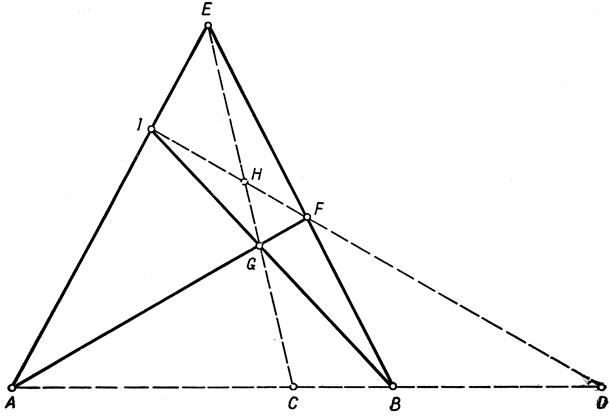
Рис. 81. Полный четырехсторонник

Как нам известно,

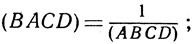
таким образом, х₂ = 1, х = ± 1. Но так как С, D разделяют Л, В,

то двойное отношение х отрицательно и потому оно должно быть равно именно -1, что мы и хотели доказать.

Полученное замечательное свойство полного четырехсторонника дает нам возможность с помощью одной лишь линейки построить точку, гармонически сопряженную с точкой С относительно пары А, В (если А, В, С коллинеарны). Нужно только, выбрав произвольную точку Е вне данной прямой, провести прямые ЕА, ЕВ, ЕС; затем, взяв произвольно точку G на ЕС, провести прямые AD и BD, пересекающие ЕВ и ЕА, скажем, в точках F и I; провести, наконец, прямую IF, которая и пересечет исходную прямую в искомой точке D.

Задача. На плоскости задан отрезок А В и область R (рис. 82). Желательно продолжить прямую АВ вправо от R. Как это можно сделать с помощью одной линейки и при условии, чтобы в процессе построения не покрывать линейкой никакой части области R? (Указание. Выберите на отрезке АВ две произвольные точки С и С', затем постройте сопряженные с ними гармонические D и D' относительно пары точек А, В; при построении воспользуйтесь четыре раза теоремой о полном четырехстороннике.)

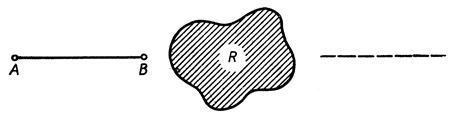
Рис. 82. Проведение прямой через препятствие