§ 3. Двойное отношение

1. Определение и доказательство инвариантности

Если длина отрезка прямой представляет собой своего рода ключ к метрической геометрии, то существует и в проективной геометрии одно основное понятие, с помощью которого могут быть выражены все отличительные проективные свойства фигур.

Предположим, что три точки А, В и С расположены на одной прямой. Проектирование, вообще говоря, изменяет не только расстояния АВ и ВС, но и их отношение 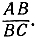В самом деле, любые три точки A, В, С на прямой l могут быть переведены в любые три точки A', В', С' на прямой l' посредством двух последовательно производимых проектирований. Чтобы в этом убедиться, станем вращать прямую l около точки С, пока она не примет положения l", параллельного l (рис. 74). Затем, проектируя l на l" параллельно прямой СС', получим три точки A", В" и С" (≡С'). Прямые А'А" и В'В" пересекутся в точке О, которую мы изберем в качестве центра второй проекции. Последовательно выполненные указанные две проекции дают требуемый результат^*.

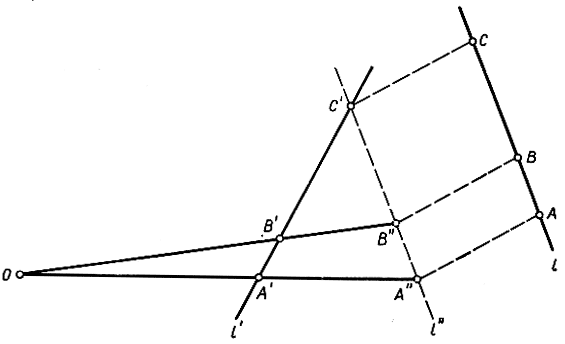
Рис. 74. Проектирование трех точек

^* (Подумайте, что делать, если прямые А'А" и В'В" параллельны.)

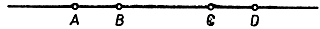
Из доказанного вытекает, что никакая величина, определяемая только тремя точками на прямой, не может быть инвариантной при проектировании. Но в этом заключается решающее открытие в проективной геометрии - если на прямой дано четыре точки A, В, С, D, которые при проектировании переходят в точки A', В', С', D' другой прямой, то некоторая величина, называемая двойным отношением этих четырех точек, при проектировании не изменяет числового значения. В этом заключено математическое свойство системы четырех точек на прямой, которое носит инвариантный характер и которое можно обнаружить во всякой проекции рассматриваемой прямой. Двойное отношение не есть ни расстояние, ни отношение расстояний, а отношение двух таких отношений: если мы составим отношения

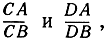
то их отношение

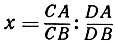
по определению есть двойное отношение четырех точек А, В, С, D, взятых в указанном выше порядке.

Убедимся теперь, что двойное отношение четырех точек инвариантно при проектировании, т. е. что если A, В, С, D и A', B', С', D' - две четверки точек на двух прямых и между ними установлено проективное соответствие, то тогда справедливо равенство

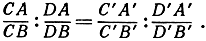
Доказательство вполне элементарно. Вспомним, что площадь треугольника равна половине произведения основания на высоту и, с другой стороны, равна половине произведения двух сторон на синус заключенного между ними угла. Тогда получим (рис. 75):

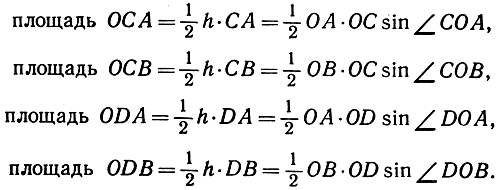
Отсюда следует:

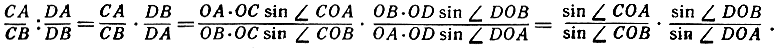
Таким образом, двойное отношение точек A, В, С, D зависит только от углов, образованных в точке О отрезками ОА, ОВ, ОС, OD. Так как эти углы - одни и те же, каковы бы ни были четыре точки A', В', С', D', в которые при проектировании переходят A, В, С, D, то ясно, что двойное отношение не изменяется при проектировании.

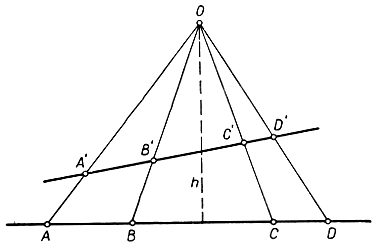
Рис. 75. Инвариантность двойного отношения при центральном проектировании

Что двойное отношение не изменяется при параллельном проектировании, следует из элементарных свойств подобных треугольников. Доказательство предоставляется читателю в качестве упражнения (рис. 76).

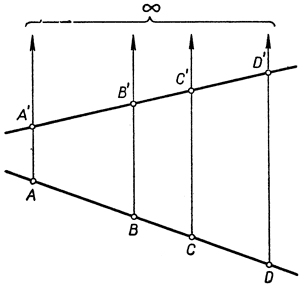
Рис. 76. Инвариантность двойного отношения при параллельном проектировании

До сих пор, говоря о двойном отношении четырех точек А, В, С, D, расположенных на прямой l, мы предполагали, что это отношение составлено из положительных отрезков. Целесообразно видоизменить это определение следующим образом. Примем одно из двух направлений прямой l за положительное и условимся, что все отрезки, отсчитываемые в этом направлении, будут считаться положительными, а отрезки, отсчитываемые в противоположном направлении,- отрицательными. Теперь определим двойное отношение точек А, B, C,D (взятых в указанном порядке) согласно формуле

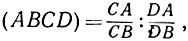
причем знаки чисел СА, СВ, DA, DB берутся в соответствии с указанным выше условием. Так как при изменении направления на прямой l, принятого за положительное, меняются только знаки всех четырех отрезков, то значение (ABCD) не зависит от выбора направления. Легко понять, что (ABCD) имеет отрицательный или положительный знак, смотря по тому, разделена ли пара точек A, В парой точек С, D или не разделена. Так как свойство "разделяться" инвариантно относительно проектирования, то понимаемое в новом смысле (как величина, способная иметь тот или иной знак) двойное отношение (ABCD) также инвариантно. Выберем начальную точку О на прямой l и сопоставим каждой точке на прямой l в качестве координаты х ее расстояние от О, взятое с надлежащим знаком; тогда, обозначая координаты A, В, C, D соответственно через х₁, х₂, х₃, х₄, получим формулу

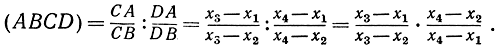
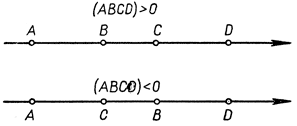
Рис. 77. Знак двойного отношения

Если (ABCD) = -1, так что ^СА/_CB = -^DA/_DB, то точки С и D делят отрезок АВ внутренне и внешне в одном и том же отношении. В этом случае принято говорить, что С и D делят отрезок АВ гармонически и каждая из точек С и D считается гармонически сопряженной с другой точкой относительно пары точек А, В. Если (ABCD) = 1, то точки С и D (или А и В) совпадают.

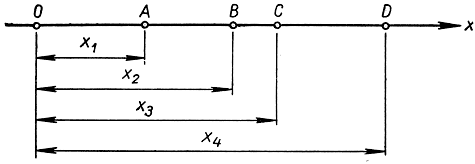
Рис. 78. Координатное выражение для двойного отношения

Необходимо не упустить из виду, что при определении двойного отношения (ABCD) существенную роль играет порядок, в котором берутся точки A, B, С, D. Например, если (ABCD) = λ, то двойное отношение (BACD) равно ¹/_λ, тогда как (DACB) = 1 - λ, в чем читатель убедится без труда. Четыре точки A, В, С, D могут быть переставлены между собой 4-3-2-1 =24 различными способами, и каждой перестановке соответствует некоторое значение двойного отношения. Некоторым перестановкам соответствует %о же числовое значение двойного отношения, что и начальной перестановке A, В, С, D; например, (ABCD) = (BADC). Предоставляем читателю в качестве упражнения доказать, что при 24 возможных перестановках четырех точек получается всего лишь шесть различных значений двойного отношения, а именно

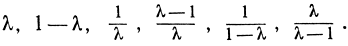
Эти шесть величин, вообще говоря, различны, но при некоторых значениях λ могут и совпадать по две, например при значении λ = -1 в случае гармонического деления.

Мы можем также определить двойное отношение четырех компланарных (т. е. лежащих в одной плоскости) и конкуррентных прямых 1, 2, 3, 4 как двойное отношение четырех точек пересечения этих прямых с некоторой прямой, лежащей в той же плоскости. Положение этой пятой прямой несущественно вследствие инвариантности двойного отношения при проектирований. Эквивалентным этому определению является следующее:

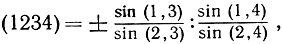
где нужно взять знак плюс, если пара прямых 1, 2 не разделяется парой 3, 4, и знак минус, если разделяется. (В этой формуле (1, 3), например, обозначает угол между прямыми 1 и 3.) Наконец, можно определить двойное отношение четырех коаксиальных плоскостей (четырех плоскостей, пересекающихся по одной прямой, или "оси"). Если некоторая прямая пересекает плоскости в четырех точках, то двойное отношение этих точек всегда будет иметь одно и то же значение, независимо от выбора прямой (доказательство предлагается в качестве упражнения). Таким образом, полученное значение можно назвать двойным отношением рассматриваемых четырех плоскостей. Иначе, можно назвать двойным отношением четырех коаксиальных плоскостей двойное отношение четырех прямых, по которым они пересекаются произвольной пятой плоскостью (рис. 79).

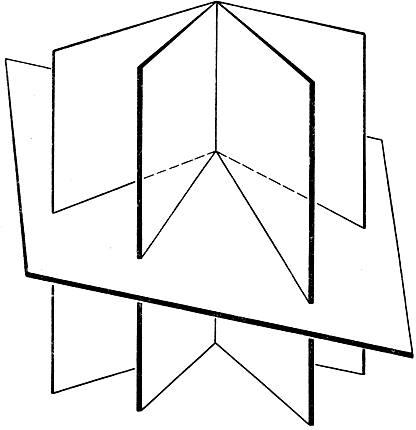
Рис. 79. Двойное отношение четырех плоскостей

Понятие двойного отношения четырех плоскостей побуждает поставить вопрос о том, нельзя ли дать определение проективного преобразования трехмерного пространства самого на себя. Определение с помощью центральной проекции, очевидно, не обобщается непосредственно от случая двух измерений на случай трех измерений. Но можно доказать, что каждое непрерывное преобразование плоскости на себя, взаимно однозначно переводящее точки в точки и прямые в прямые, есть проективное преобразование. Это обстоятельство наводит на мысль ввести следующее определение для случая трех измерений: проективным преобразованием пространства называется непрерывное взаимно однозначное преобразование, переводящее прямые линии в прямые линии. Можно показать, что такие преобразования оставляют значения двойных отношений неизменными.

Добавим к предыдущему еще кое-какие замечания. Пусть на прямой даны три различные точки A, В, С с координатами х₁, х₂, х₃. Требуется найти четвертую точку D таким образом, чтобы удовлетворялось равенство (ABCD) = λ, где λ задано. (Частный случай, когда λ = - 1 и задача заключается в построении четвертой гармонической точки, будет подробно рассмотрен в следующем пункте.) Вообще говоря, задача имеет одно и только одно решение; действительно, если х - координата искомой точки D, то уравнение

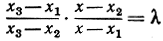
имеет ровно одно решение. Считая х₁, х₂ и х₃ заданными и полагая ради краткости 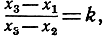мы придадим решению вид

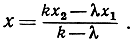
Например, если точки А, В, С находятся на равных расстояниях друг от друга и имеют соответственно координаты х₁ = 0, х₂ = d, x₃ = 2d, то тогда

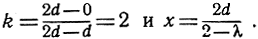
Если прямая l спроектирована из двух различных центров О' и О" на две различные прямые l' и l", то получается соответствие Р↔P' между точками прямых l и l' и соответствие Р↔Р" между точками прямых l и l". Этим устанавливается соответствие Р'↔P" между точками прямых l' и l" и притом такое, что каждые четыре точки А', В', С', D' на l' имеют то же самое двойное отношение, что и соответствующие точки A", В", С", D" на l". Всякое взаимно однозначное соответствие между точками двух прямых, обладающее этим свойством, называется проективным соответствием, независимо от того, каким способом это соответствие установлено.

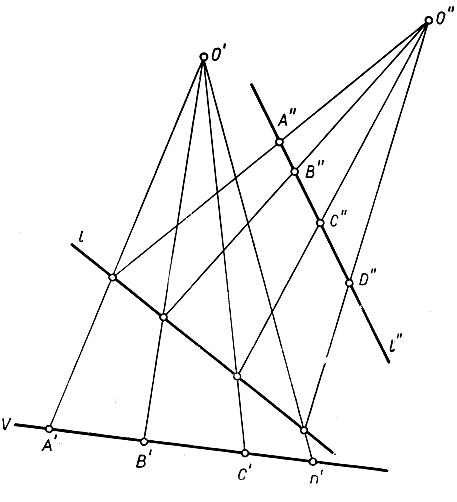
Рис. 80. Проективное соответствие между точками двух прямых

Упражнения.

1. Доказать, что если даны две прямые вместе с проективным соответствием, установленным между ними, то можно подвергнуть одну из прямых такому параллельному перенесению, что заданное соответствие будет получаться посредством простой проекции. (Указание. Совместите какую-нибудь пару взаимно соответствующих точек на данных прямых.)
2. Пользуясь предыдущим результатом, показать, что если между точками двух прямых l и l' установлено соответствие посредством конечного числа последовательных проектирований на различные промежуточные прямые при произвольных центрах проекций, то тот же результат может быть получен посредством всего лишь двух проектирований.