2. Теорема Дезарга

Одним из самых ранних открытий в области проективной геометрии является замечательная теорема Дезарга (1593-1662):Если на плоскости два треугольника ABC и А'В'С расположены таким образом у что прямые, соединяющие соответственные вершины, конкуррентны, то три точки, в которых пересекаются, будучи продолжены, три соответственные стороны,- коллинеарны. Эта теорема здесь иллюстрируется чертежом (рис. 72), но пусть читатель проверит ее справедливость, экспериментируя на самостоятельно построенных чертежах. Доказательство теоремы не является тривиальным, несмотря на всю простоту чертежа, состоящего только из прямых линий. Теорема явственно принадлежит проективной геометрии, так как при проектировании рассматриваемый чертеж не теряет свойств, упомянутых в теореме. В дальнейшем мы еще вернемся к этой теореме (стр. 218). В настоящий же момент мы хотели бы привлечь внимание читателя к тому любопытному обстоятельству, что теорема Дезарга справедлива также и в том предположении, что рассматриваемые треугольники расположены в двух различных (непараллельных) плоскостях и что подобного рода "трехмерная", или "пространственная", теорема Дезарга доказывается без малейших затруднений. По предположению, прямые АА', ВВ' и СС пересекаются в одной и той же точке Q (рис. 73). В таком случае прямые АВ и А'В' лежат в одной плоскости и, значит, пересекаются в некоторой точке R; пусть таким же образом АС и А'С пересекаются в точке Q, а ВС и В'С - в точке Р. Так как точки Р, Q и R находятся на продолжениях сторон треугольников ABC и А'В'С, то все они лежат в плоскости каждого из этих треугольников и потому - на прямой пересечения этих двух плоскостей. Значит, Р, Q и R коллинеарны, что и требовалось доказать.

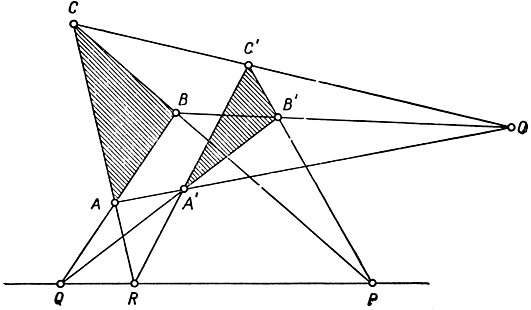
Рис. 72. Конфигурация Дезарга на плоскости

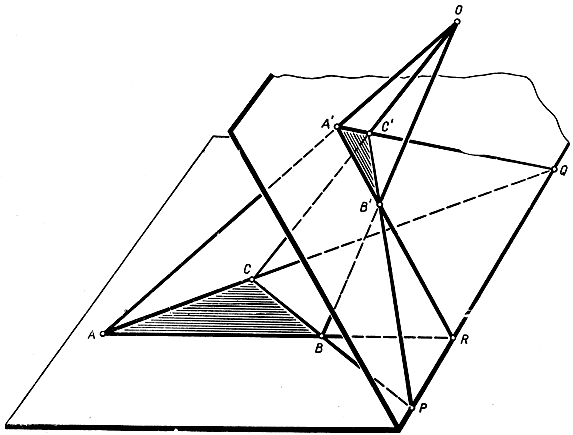
Рис. 73. Конфигурация Дезарга в пространстве

Это простое доказательство наводит на мысль, что можно было бы попытаться доказать "двумерную" теорему Дезарга, так сказать, с помощью перехода к пределу, постепенно сплющивая всю пространственную конструкцию таким образом, чтобы две плоскости в пределе совпали в одну, и в этой последней, вместе с другими, оказалась и точка О. Выполнить, однако, указанный предельный переход не так просто, так как прямая пересечения PQR при совмещении плоскостей не определяется однозначно. Тем не менее конфигурация, изображенная на рис. 72, может быть истолкована как перспективное изображение пространственной конфигурации рис. 73, и это обстоятельство можно использовать при доказательстве "плоской" теоремы.

Есть существенное различие между теоремой Дезарга на плоскости и в пространстве. Наше доказательство, относящееся к случаю трех измерений, опиралось только на геометрические соображения, относящиеся к инцидентности точек, прямых и плоскостей. Можно показать, что доказательство двумерной теоремы - при дополнительная требовании не выходить из данной плоскости - неизбежно должно опираться на некоторые свойства подобных фигур, принадлежащих уже не проективной, а метрической геометрии.

Теорема, обратная теореме Дезарга, утверждает, что если три точки, в которых пересекаются соответственные стороны, коллинеарны, то прямые, соединяющие соответственные вершины, конкуррентны. Доказательство этой теоремы - в случае, когда треугольники лежат в непараллельных плоскостях,- предоставляется читателю в качестве упражнения.