§ 2. Основные понятия

1. Группа проективных преобразований

Прежде всего определим класс, или "группу"^*, проективных преобразований. Пусть в пространстве заданы две плоскости π и π', параллельные или непараллельные между собой. Мы выполняем центральную проекцию π на π' с данным центром О, не лежащим ни на π, ни на π', сопоставляя каждой точке Р плоскости π такую точку Р' плоскости π', что Р и Р' лежат на одной и той же прямой, проходящей через О. Аналогично мы выполняем параллельную проекцию, предполагая, что проектирующие прямые параллельны между собой. Точно так же определяется проекция прямой или кривой линии l в плоскости π на некоторую линию l' в плоскости π', причем и в этом случае проекция может быть центральной или параллельной.

^* (Термин "группа" в применении к классу преобразований подразумевает, что последовательное выполнение двух преобразований из рассматриваемого класса есть также преобразование этого класса и что преобразование, "обратное" по отношению к преобразованию из рассматриваемого класса, также принадлежит этому классу. Групповые свойства математических операций играли и продолжают играть очень большую роль во многих областях, однако по отношению к геометрии значение понятия "группы" в свое время, возможно, было несколько преувеличено.)

Всякое отображение одной фигуры на другую, получающееся посредством проектирования (центрального или параллельного) или же посредством конечной последовательности таких проектирований, называется проективным преобразованием^*. Проективная геометрия плоскости или прямой состоит из системы геометрических теорем, сохраняющихся при произвольных проективных преобразованиях соответствующих фигур. Проективной геометрии противопоставляется метрическая геометрия, которая понимается как система теорем, устанавливающих связи между величинами в рассматриваемых фигурах, инвариантные только относительно класса движений.

^* (Если две фигуры связаны только одним проектированием, то говорят обычно, что они перспективны. Таким образом, если сказано, что фигура F в результате проективного преобразования переходит в фигуру F', то это значит, что или фигуры F и F' перспективны, или же можно указать последовательность таких фигур F, F₁, F₂, ..., F_n, F', что любые две рядом стоящие в ней фигуры перспективны.)

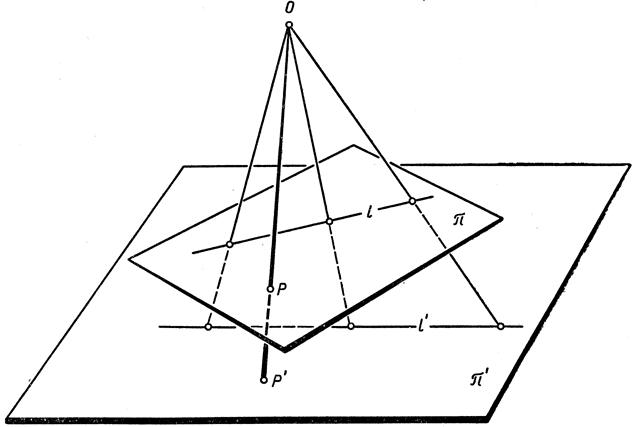
Рис. 70. Центральная проекция

Некоторые проективные свойства можно формулировать непосредственно. Точка, разумеется, проектируется в точку. Далее, прямая линия проектируется в прямую: в самом деле, если прямая l в плоскости я проектируется на плоскость π', то линия пересечения l' плоскости π с плоскостью, проходящей через О и l,- обязательно прямая^*. Если точка А и прямая l инцидентны^**, то точка А' и прямая l', возникающие из них при проективном преобразовании, также инцидентны. Другими словами, инцидентность точки и прямой есть свойство, инвариантное относительно группы проективных преобразований. Из этого обстоятельства вытекает ряд простых, но весьма важных следствий. Если три точки (или более трех точек) коллинеарны, т. е. инцидентны с одной и той же прямой, то их отображения также коллинеарны. Аналогично, если в плоскости я три прямые (или более трех прямых) конкуррентны, т. е. инцидентны с одной и той же точкой, то их отображения - также конкуррентные прямые. В то время как эти простые свойства - инцидентность, коллинеарность, конкуррентность - являются проективными свойствами (т. е. свойствами, инвариантными относительно проективных преобразований), величины отрезков и углов, а также и отношения этих величин, вообще говоря, изменяются при проектировании. Равнобедренные или равносторонние треугольники могут, например, спроектироваться на треугольники с тремя различными сторонами. Отсюда следует, что, хотя понятие "треугольник" принадлежит проективной геометрии, понятие "равносторонний треугольник" ей не принадлежит, а принадлежит только метрической геометрии.

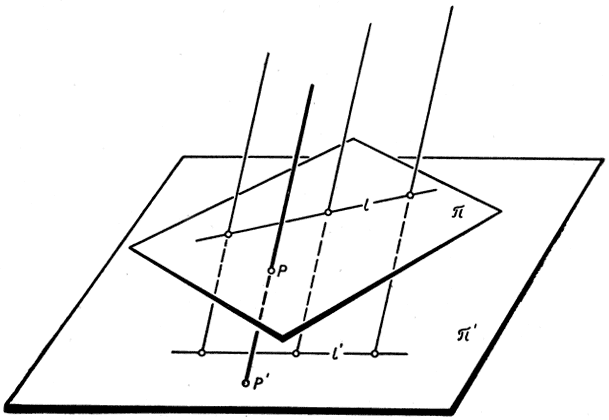
Рис. 71. Параллельная проекция

^* (За исключением того случая, когда прямая ОР (или плоскость, проходящая через О и l) оказывается параллельной плоскости π. Такие исключения будут устранены в § 4.)

^** (Точка и прямая называются инцидентными, если прямая проходит через точку или точка лежит на прямой. Этот "нейтральный" термин подчеркивает взаимность рассматриваемого отношения.)