2. Применение к проблеме Аполлония

Прекрасной иллюстрацией того, насколько полезна теория инверсии, является следующее простое геометрическое решение проблемы Аполлония. При инверсии относительно какого бы то ни было центра проблема Аполлония для трех данных окружностей трансформируется в соответствующую проблему для трех других окружностей: пусть читатель внимательно продумает, почему это так.

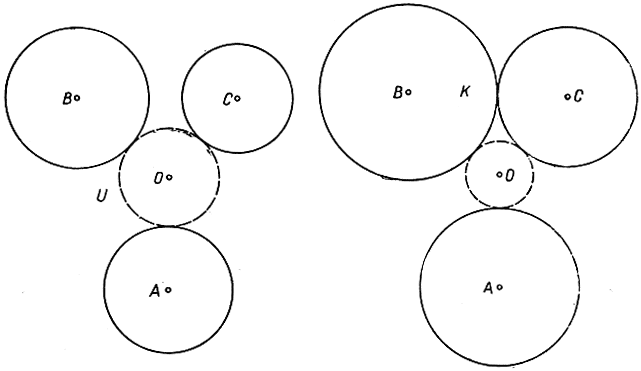
Рис. 63. Подготовка построения, решающего проблему Аполлония

Отсюда легко понять, что если проблема решена для некоторой тройки окружностей, то тем самым ее можно считать решенной и для всякой тройки окружностей, которая из первой тройки может быть получена путем инверсии. Мы сумеем использовать это обстоятельство, выбирая из всевозможных "эквивалентных" троек такую, для которой проблема решается особенно просто.

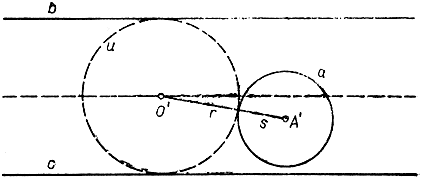
Рис. 64. Решение проблемы Аполлония

Предположим для определенности, что три данные окружности с центрами A, В, С взаимно не пересекаются и лежат каждая вне двух других, и допустим, что речь идет о нахождении окружности U с центром О и радиусом р, касающейся трех данных окружностей внешним образом. Заметим, что если мы увеличим радиус всех трех данных окружностей на одну и ту же величину d, то окружность с центром О и радиусом р - d, очевидно, была бы решением видоизмененной таким образом проблемы. Пользуясь этим обстоятельством, увеличим радиусы данных окружностей на такую величину, чтобы две из трех окружностей оказались взаимно касающимися в некоторой точке, которую обозначим K (рис. 63). Затем произведем инверсию всей фигуры относительно какой-нибудь окружности с центром K. Окружности с центрами В и С станут параллельными прямыми b и с, а третья окружность превратится в некоторую окружность а (рис. 64). Мы уже знаем, что а, b, с могут быть построены с помощью циркуля и линейки. Что касается искомой окружности U, то она преобразуется в окружность и, касающуюся прямых b, с и окружности а. Его радиус r, очевидно, должен равняться половине расстояния между прямыми b и с; центр же его О' должен совпадать с одной из точек пересечения средней линии между b и с с окружностью, концентрической окружности а, но имеющей радиус на r больший. Остается применить обратную инверсию к окружности u, и тогда получим искомую аполлониеву окружность U.