§ 6. Еще об инверсии и ее применениях

1. Инвариантность углов. Семейства окружностей

Хотя круговая инверсия есть преобразование, довольно резко меняющее внешний вид геометрических фигур, все же весьма замечательным является то обстоятельство, что вновь получаемые фигуры сохраняют некоторые свойства первоначальных фигур. Эти свойства, не теряющиеся при преобразовании, называются инвариантными. Мы уже знаем, что при инверсии окружность или прямая переходит в окружность или прямую. Прибавим теперь еще одно важное свойство инверсии: угол между двумя прямыми или кривыми при инверсии не изменяется. Говоря подробнее, это означает, что инверсия преобразовывает две пересекающиеся кривые в две другие кривые, которые пересекаются под тем же углом. Под углом между кривыми подразумевается угол между их касательными.

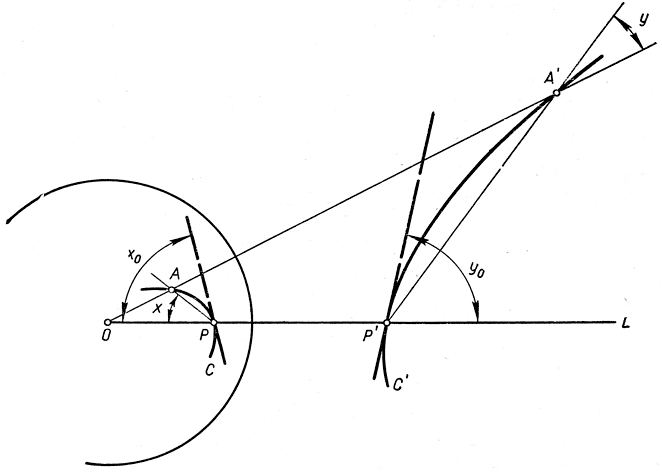
Рис. 60. Инвариантность углов при инверсии

Доказательство получается при рассмотрении рис. 60, где имеется в виду частный случай пересечения в точке Р произвольной кривой С с прямолинейным отрезком OL, проведенным из центра инверсии О. Кривая С, обратная кривой С, пересекается с OL в точке Р', обратной Р, так как Р', так же как и Р, лежит на OL. Покажем, что угол x₀ между OL и касательной к С в точке Р по величине равен углу y₀ между OL и касательной к С в точке Р'. Для этого возьмем точку А на кривой С вблизи Р и проведем секущую АР.

Точка, обратная A, есть А'; так как она находится на прямой ОА и на кривой С, то является их точкой пересечения. Проведем также секущую А'Р'. По определению инверсии r² = ОР*ОР' = ОА*ОА', или же

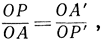
т. е. треугольники ОАР и ОА'Р' подобны. Значит, угол х равен углу ОА'Р', который мы обозначим через y. Последний шаг в нашем рассуждении заключается в том, чтобы заставить точку А приближаться по кривой С к точке Р. При этом секущая АР переходит в касательную к кривой С в точке Р и угол x: стремится к х₀. В то же время А' будет приближаться к Р' и прямая А'Р' перейдет в касательную к кривой С' в точке Р', а угол y будет стремиться к у₀. Так как при всяком положении точки А мы имеем равенство х = y, то оно сохранится и в пределе х₀ = y₀.

Наше доказательство еще не закончено, так как мы рассмотрели пока только случай пересечения кривой С с прямой, проходящей через центр О. Но рассмотреть общий случай пересечения двух произвольных кривых С и С' теперь уже совсем легко. Пусть эти кривые пересекаются в точке Р и образуют между собой угол z. Тогда прямая ОРР' делит этот угол на два угла, из которых каждый в отдельности не изменяется при инверсии.

Следовало бы оговорить, что, хотя инверсия не изменяет величины угла, однако, она изменяет направление его отсчета: если вообразим, что при постоянном увеличении угла x₀ одна сторона его неподвижна, а другая вращается против часовой стрелки, то подвижная сторона соответствующего "обратного" угла вращается по часовой стрелке.

Частным следствием инвариантности углов при инверсии является то, что две ортогональные (т. е. пересекающиеся под прямым углом) окружности или прямые после инверсии сохраняют это свойство, и если две окружности взаимно касаются ("пересекаются под углом, равным нулю"), то касаются и обратные им окружности.

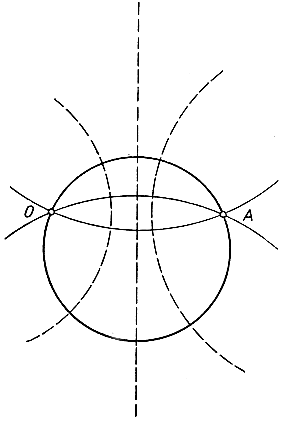
Рис. 61. Преобразование двух систем ортогональных окружностей с помощью инверсии

Рассмотрим семейство окружностей, проходящих через центр инверсии О и еще через одну и ту же неподвижную точку плоскости А. Мы знаем (§ 4, пункт 2), что это семейство преобразуется в семейство прямых, проходящих через точку A', являющуюся образом A. В то же время семейство окружностей, ортогональных первоначальному семейству, превращается в семейство окружностей, ортогональных упомянутому семейству прямых. (На рис. 61 ортогональные семейства изображены пунктиром.) С внешней стороны семейство прямых, проходящих через одну и ту же точку, мало напоминает семейство окружностей, но эти семейства связаны теснейшим образом - с точки зрения теории инверсии они, так сказать, вполне эквивалентны.

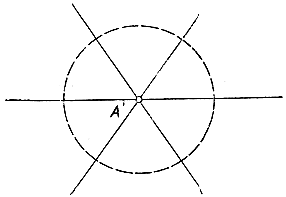
Рис. 62. Преобразование касающихся окружностей в параллельные прямые

Вот другой пример того, к каким результатам приводит инверсия. Пусть дано семейство окружностей, проходящих через центр инверсии и имеющих в этой точке общую касательную. После инверсии получается семейство параллельных прямых. Действительно, так как окружности проходят через точку О, то они превращаются в прямые, а так как окружности, кроме О, не имеют точек пересечения, то получаемые прямые - параллельны.