*4. Шарнирные механизмы. Инверсоры Поселье и Гарта

Оставим на время в стороне вопрос о циклоидах (они появятся еще раз в этой книге - довольно неожиданно) и обратимся к иным методам механического воспроизведения кривых линий. Мы займемся сейчас шарнирными механизмами.

Механизм этого типа представляет собой систему сочлененных между собой твердых стержней, обладающих такой степенью свободы, чтобы каждая его точка была способна описывать определенную кривую. Циркуль также является простейшим шарнирным механизмом, по существу состоящим из одного стержня с закрепленным концом.

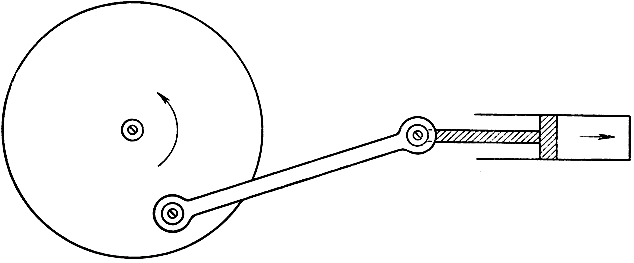
Рис. 57. Преобразование прямолинейного движения во вращательное

Шарнирные механизмы издавна находят себе применение как составные части машин. Одним из самых знаменитых (в историческом отношении) примеров является так называемый "параллелограмм Уатта". Это приспособление было изобретено Джемсом Уаттом при решении следующей проблемы: как связать поршень с точкой махового колеса таким образом, чтобы вращение колеса сообщало поршню прямолинейное движение? Решение, данное Уаттом, было лишь приближенным, и, несмотря на усилия многих первоклассных математиков, проблема конструирования механизма, сообщающего точке в точности прямолинейное движение, долгое время оставалась нерешенной. Было даже сделано предположение, что такой механизм неосуществим: это было как раз тогда, когда всякого рода "доказательства невозможности" привлекли к себе всеобщее внимание. Тем большее изумление было вызвано в кругах математиков, когда французский морской офицер Поселье (в 1864 г.) все же изобрел несложный механизм, действительно разрешающий проблему в положительном смысле. В связи с введением в употребление хорошо действующих смазочных веществ техническая проблема потеряла свое значение для паровых машин.

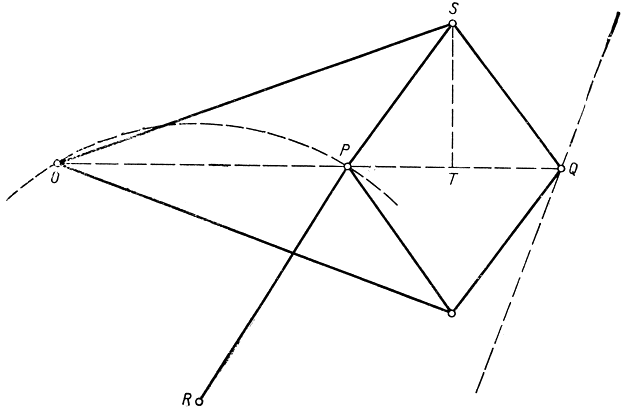
Рис. 58. Инверсор Поселье, преобразующий вращательное движение в прямолинейное

Назначение механизма Поселье заключается в том, чтобы превращать круговое движение в прямолинейное. В основе этого механизма лежит теория инверсии, изложенная в § 4. Как видно из рис. 58, механизм состоит из семи жестких стержней, два из них - длины t, четыре - длины в и один - произвольной длины. Точки О и R закреплены и расположены таким образом, что OR = PR. Весь аппарат может быть приведен в движение, будучи подчинен указанным условиям. Мы сейчас убедимся, что, когда точка Р описывает дугу окружности с центром R и радиусом RP, точка Q описывает прямолинейный отрезок. Обозначая основание перпендикуляра, опущенного из точки S на прямую OPQ, через T мы замечаем, что

Величина t² - s² постоянная; положим t² - s² = r². Так как OP*OQ = r², то точки Р и Q взаимно обратные относительно окружности с центром О и радиусом r. В то время как Р описывает дугу окружности, проходящей через О, Q описывает кривую, обратную этой дуге. Но кривая, обратная окружности, проходящей через О, есть, как мы видели, не что иное, как прямая линия. Итак, траектория точки Q есть прямая, и инверсор Поселье чертит эту прямую без линейки.

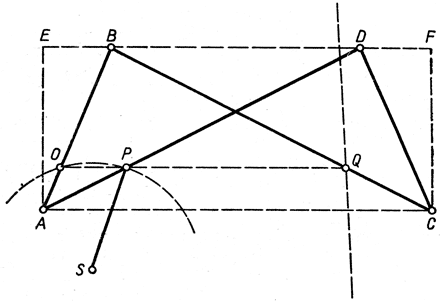
Рис. 59. Инверсор Гарта

Другой механизм, решающий ту же проблему, есть инверсор Гарта. Он состоит всего лишь из пяти стержней, сочленение которых показано на рис. 59. Здесь АВ = CD, ВС = AD. Через О, Р и Q обозначены точки, соответственно зафиксированные на стержнях АВ, AD и СВ, притом таким образом, что 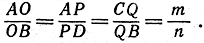Точки О и S закреплены на плоскости неподвижно, с соблюдением условия OS = PS. Больше связей нет, и механизм способен двигаться. Очевидно, прямая АС всегда параллельна прямой BD. В таком случае точки О, Р и Q лежат на одной прямой, и прямая ОР параллельна прямой АС. Проведем перпендикуляры АЕ и CF к прямой BD. Мы имеем:

Но ED² + АЕ² = AD² и ЕВ² + АЕ² = АВ². Значит, ED² - ЕВ² = AD² - АВ₂. Далее,

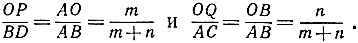
Следовательно,

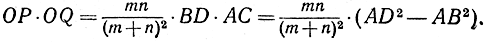
Последняя полученная величина не изменяется при движении механизма. Поэтому точки Р и Q являются взаимно обратными относительно некоторой окружности с центром О. При движении механизма точка Р описывает окружность с центром S, проходящую через О; значит, обратная точка Q описывает прямую линию.

Можно построить - по крайней мере теоретически - другие шарнирные механизмы, которые будут чертить эллипсы, гиперболы и даже любую наперед заданную алгебраическую кривую f(x, y) = 0, какова бы ни была ее степень.