3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды

Изобретение различных механизмов, предназначенных для того, чтобы чертить различные кривые, помимо окружности и прямой линии, чрезвычайно расширяет область фигур, допускающих построение. Например, если имеется инструмент, позволяющий чертить гиперболы хy = k, и другой инструмент, вычерчивающий параболы y = ах² + bх + с, то любая проблема, приводящая к кубическому уравнению

может быть решена конструктивно, с помощью только этих инструментов. В самом деле, решение уравнения (1) равносильно решению системы

точнее, корни уравнения (1) являются х-координатами точек пересечения гиперболы и параболы, представляемых уравнениями (2). Таким образом, решения уравнения (1) допускают построение, если разрешается пользоваться инструментами, с помощью которых можно начертить кривые (2).

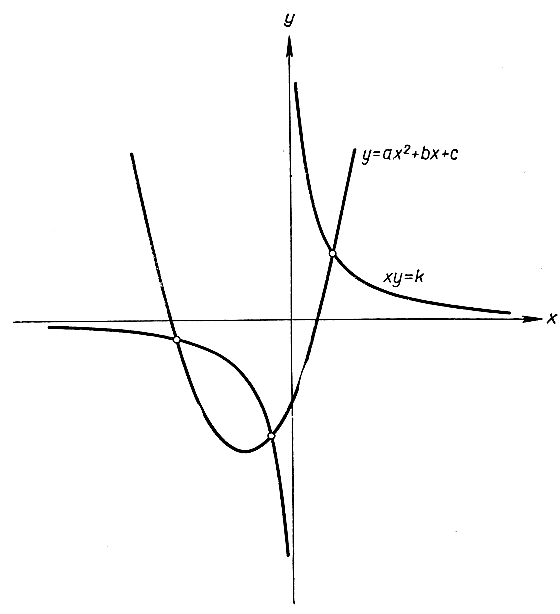
Рис. 52. Графическое решение кубического уравнения

Уже математикам древности были известны многие интересные кривые, которые могут быть определены и начерчены с помощью простых механических приспособлений. Среди таких "механических" кривых особенно видное место занимают циклоиды. Птолемей (около 200 г. до нашей эры), обнаруживая необычайную проницательность, сумел использовать эти кривые для описания планетных движений.

Рис. 53. Циклоида

Циклоида самого простого вида представляет собой траекторию движения очки Р, фиксированной на окружности диска, катящегося без скольжения по прямой линии. На рис. 53 изображены четыре положения точки Р в различные моменты времени. С внешней стороны циклоида напоминает ряд арок, опирающихся на горизонтальную прямую.

Разновидности этой кривой получаются, если возьмем точку Р или внутри диска (как на спице колеса), или на продолжении радиуса за пределы диска.

Эти две кривые показаны на рис. 54.

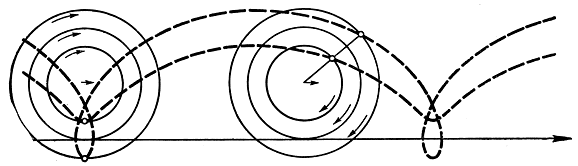
Рис. 54. Циклоиды общего вида

Дальнейшие разновидности циклоиды возникают, когда наш диск катится не по прямой, а по дуге окружности. Если при этом катящийся диск с радиусом к остается все время касающимся изнутри той большой окружности С радиуса R, по которой он катится, то траектория точки, фиксированной на окружности диска, называется гипоциклоидой.

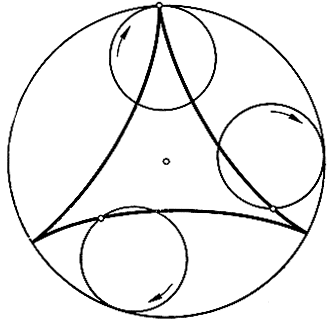
Рис. 55. Трехрогая гипоциклоида

Когда диск прокатывается по всей окружности С ровно один раз, то точка Р возвращается в исходное положение только в том случае, если радиус С является кратным радиуса с. На рис. 55 изображена замкнутая гипоциклоида, соответствующая предположению R = 3r. В более общем случае, если 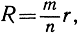то гипоциклоида замкнется после того, как диск с прокатится по окружности С ровно n раз, и будет состоять из m арок. Заслуживает особого упоминания случай R = 2r. Любая точка Р на окружности диска будет описывать в этом случае один из диаметров большой окружности С (рис. 56). Предоставляем читателю доказать это в качестве задачи.

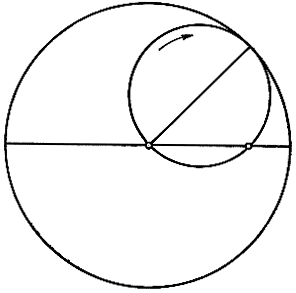
Рис. 56. Прямолинейное движение при качении круга по окружности двойного радиуса

Еще один тип циклоид получается, когда диск с катится по окружности С, касаясь ее все время извне. Получающиеся при этом кривые носят название эпициклоид.