2. Построения с помощью одного циркуля

Если вполне естественно, что с допущением большего разнообразия инструментов оказывается возможным решать более обширное множество задач на построение, то можно было бы предвидеть, что, напротив, при ограничениях, налагаемых на инструменты, класс разрешимых задач будет суживаться. Тем более замечательным нужно считать открытие, сделанное итальянцем Маскерони (1750-1800):все геометрические построения, выполнимые с помощью циркуля и линейки, могут быть выполнены с помощью одного только циркуля. Следует, конечно, оговорить, что провести на самом деле прямую линию через две данные точки без линейки невозможно, так что это основное построение не покрывается теорией Маскерони. Вместо того приходится считать, что прямая задана, если заданы две ее точки. Но с помощью одного лишь циркуля удается найти точку пересечения двух прямых, заданных таким образом, или точку пересечения прямой с окружностью.

Вероятно, простейшим примером построения Маскерони является удвоение данного отрезка АВ. Решение было уже дано на стр. 174-175. Далее, на стр. 175-176 мы научились делить данный отрезок пополам. Посмотрим теперь, как разделить пополам дугу окружности АВ с центром О. Вот описание этого построения (рис. 47). Радиусом АО проводим две дуги с центрами A и В. От точки О откладываем на этих дугах две такие дуги ОР и OQ, что OP = OQ = АВ. Затем находим точку R пересечения дуги с центром Р и радиусом РВ и дуги с центром Q и радиусом QA. Наконец, взяв в качестве радиуса отрезок OR, опишем дугу с центром Р или Q до пересечения с дугой AВ - точка пересечения и является искомой средней точкой дуги АВ. Доказательство предоставляем читателю в качестве упражнения.

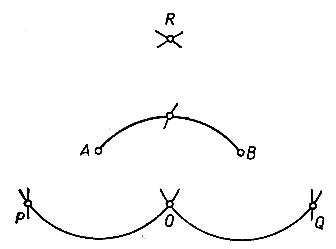
Рис. 47. Нахождение середины дуги без линейки

Было бы невозможно доказать основное утверждение Маскерони, указывая для каждого построения, выполнимого с помощью циркуля и линейки, как его можно выполнить с помощью одного циркуля: ведь возможных построений бесчисленное множество. Но мы достигнем той же цели, если установим, что каждое из следующих основных построений выполнимо с помощью одного циркуля:

1. Провести окружность, если заданы ее центр и радиус.
2. Найти точки пересечения двух окружностей.
3. Найти точки пересечения прямой и окружности.
4. Найти точку пересечения двух прямых.

Любое геометрическое построение (в обычном смысле, с допущением циркуля и линейки) составляется из выполнения конечной последовательности этих элементарных построений. Что первые два из них выполнимы с помощью одного циркуля, ясно непосредственно. Более трудные построения 3 и 4 выполняются с использованием свойств инверсии, рассмотренных в предыдущем пункте.

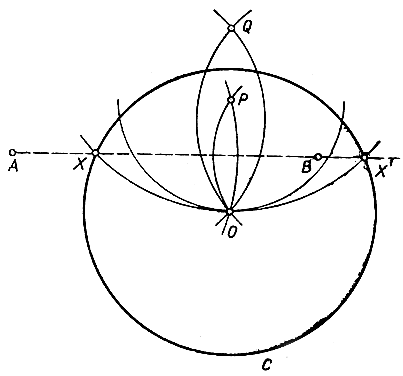
Рис. 48. Пересечение окружности и прямой, не проходящей через центр

Обратимся к построению 3: найдем точки пересечения данного круга С с прямой, проходящей через данные точки А и В. Проведем дуги с центрами А и В и радиусами, соответственно равными АО и ВО, кроме точки О, они пересекутся в точке Р. Затем построим точку Q, обратную точке Р относительно окружности С (см. построение, описанное на стр. 174). Наконец, проведем окружность с центром Q и радиусом QO (она непременно пересечется с С): ее точки пересечения Х и Х' окружностью С и будут искомыми. Для доказательства достаточно установить, что каждая из точек X и X' находится на одинаковых расстояниях от О и P (что касается точек А и В, то аналогичное их свойство сразу вытекает из построения). Действительно, достаточно сослаться на то обстоятельство, что точка, обратная точке Q, отстоит от точек X и Х' на расстояние, равное радиусу круга С (см. стр. 173). Стоит отметить, что окружность, проходящая через точки X, X' и О, является обратной прямой АВ в инверсии относительно окружности С, так как эта окружность и прямая АВ пересекаются с С в одних и тех же точках. (При инверсии точки основной окружности остаются неподвижными.) Указанное построение невыполнимо только в том случае, если прямая АВ проходит через центр С. Но тогда точки пересечения могут быть найдены посредством построения, описанного на стр. 178, как середины дуг С, получающихся, когда мы проводим произвольную окружность с центром В, пересекающуюся с С в точках В₁ и В₂.

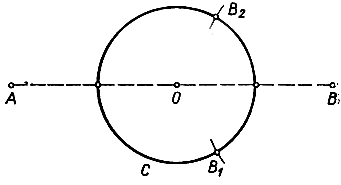
Рис. 49. Пересечение окружности и прямой, проходящей через центр

Метод проведения окружности, обратной прямой," соединяющей две данные точки, немедленно дает и построение, решающее задачу 4. Пусть прямые даны точками А, В и A', В' (рис. 50) Проведем произвольную окружность С и с помощью указанного выше метода построим окружности, обратные прямым АВ и А'В'. Эти окружности пересекаются в точке О и еще в одной точке Y, Точка X, обратная точке Y, и есть искомая точка пересечения: как ее построить - уже было разъяснено выше. Что X есть искомая точка, это ясно из того факта, что Y есть единственная точка, обратная точке, одновременно принадлежащей обеим прямым АВ и А'В', следовательно, точка X, обратная Y, должна лежать одновременно и на АВ, и на А'В'.

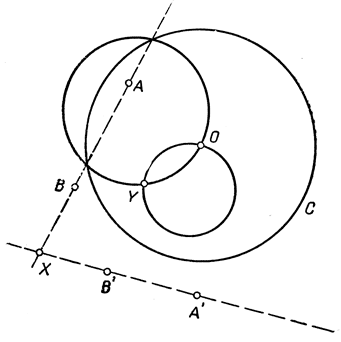
Рис 50. Пересечение двух прямых

Этими двумя построениями заканчивается доказательство эквивалентности между построениями Маскерони, при которых разрешается пользоваться только циркулем, и обыкновенными геометрическими построениями с циркулем и линейкой.

Мы не заботились об изяществе решения отдельных проблем, нами здесь рассмотренных, так как нашей целью было выяснить внутренний смысл построений Маскерони. Но в качестве примера мы еще укажем построение правильного пятиугольника; точнее говоря, речь идет о нахождении каких-то пяти точек на окружности, которые могут служить вершинами правильного вписанного пятиугольника.

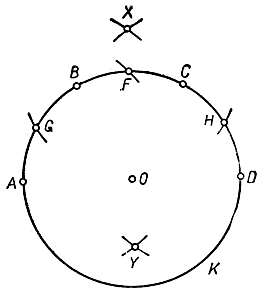
Рис. 51. Построение правильного пятиугольника

Пусть Л- произвольная точка на окружности К. Так как сторона правильного вписанного шестиугольника равна радиусу круга, то не представит труда отложить на К такие точки В, С, D, что АВ = ВС = CD = 60° (рис. 51). Проводим дуги с центрами А и D радиусом, равным АС; пусть они пересекаются в точке X. Тогда, если О есть центр K, дуга с центром А и радиусом ОХ пересечет К в точке F, являющейся серединой дуги ВС (см. стр. 178). Затем радиусом, равным радиусу K, опишем дуги с центром F, пересекающиеся с K в точках G и H. Пусть Y есть точка, расстояния которой от точек G и Н равны ОХ и которая отделена от X центром О. В таком случае отрезок AY как раз и есть сторона искомого пятиугольника. Доказательство предоставляется читателю в качестве упражнения. Интересно отметить, что при построении используются только три различных радиуса.

В 1928 г. датский математик Ельмслев нашел в книжной лавке в Копенгагене экземпляр книги под названием Euclides Danicus, опубликованной в 1672 г. никому не известным автором Г. Мором. По титульному листу можно было сделать заключение, что это просто один из вариантов евклидовых "Начал", снабженный, может быть, редакторским комментарием. Но по внимательном рассмотрении оказалось, что в ней содержится полное решение проблемы Маскерони, найденное задолго до Маскерони.

Упражнения. В дальнейшем дается описание построений Мора. Проверьте их правильность. Почему можно утверждать, что они решают проблему Маскерони?

1. К отрезку AВ длины р восставить перпендикуляр ВС. (Указание. Продолжить AВ до точки D таким образом, что AВ = BD. Провести произвольным радиусом дуги с центрами А и D и таким образом определить С.)
2. В плоскости даны как угодно расположенные отрезки длины р и q, причем p>q. Построить с помощью 1) отрезок длины
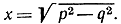
3. По заданному отрезку а построить отрезок a√2. (Указание. Обратите внимание, что (а√2)² = (а√3)² - а².)
4. По данным отрезкам р и q построить отрезок 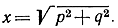(Указание. Примите во внимание, что х² = 2р² - (р² - q²).) Придумайте сами аналогичные построения.
5. Пользуясь предыдущими результатами, постройте отрезки р + q и р - q, предполагая, что отрезки длины р и q заданы как-то на плоскости.
6. Проверьте и постарайтесь обосновать следующее построение середины М данного отрезка AВ длины а. На продолжении отрезка AВ найдем такие точки С и D, что СA = AВ = BD. Построим равносторонний треугольник ECD согласно условию ЕС = ED = 2а и определим М как пересечение окружностей с диаметрами ЕС и ED.
7. Найти прямоугольную проекцию точки А на отрезок ВС.
8. Найти х по условию х:а = р:q, где а, р и q - данные отрезки.
9. Найти х = ab, где а и b - данные отрезки.

Вдохновляясь результатами Маскерони, Якоб Штейнер (1796-1863) предпринял попытку исследования построений, выполнимых с помощью одной только линейки. Конечно, одна только линейка не выводит за пределы данного числового поля, и потому она недостаточна для выполнения всех геометрических построений в классическом их понимании. Но тем более замечательны результаты, полученные Штейнером при введенном им ограничении - пользоваться циркулем только один раз. Он доказал, что все построения на плоскости, выполнимые с помощью циркуля и линейки, выполнимы также с помощью одной линейки при условии, что задан единственный неподвижный круг вместе с центром. Эти построения подразумевают применение проективных методов и будут описаны позднее (см. стр. 228).

^*Без круга, и притом с центром, обойтись нельзя. Например, если дан круг, но не указан его центр, то найти центр с помощью одной линейки невозможно. Мы сейчас докажем это, ссылаясь, однако, на факт, который будет установлен позднее (см. стр. 252): существует такое преобразование плоскости самой в себя, что а) заданная окружность остается неподвижной, b) всякая прямая линия переходит в прямую, с) центр неподвижной окружности не остается неподвижным, а смещается. Само существование такого преобразования свидетельствует о невозможности построить центр данной окружности, пользуясь одной линейкой. В самом деле, какова бы ни была процедура построения, она сводится к ряду отдельных этапов, заключающихся в проведении прямых линий и нахождении их пересечений друг с другом или с данной окружностью. Представим себе теперь, что вся фигура в целом - окружность, а все прямые, проведенные по линейке при выполнении построения центра, подвергнуты преобразованию, существование которого мы здесь допустили. Тогда ясно, что фигура, полученная после преобразования, также удовлетворяла бы всем требованиям построения; но указываемое этой фигурой построение приводило бы к точке, отличной от центра данной окружности. Значит, построение, о котором идет речь, невозможно.