§ 5. Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля

*1. Классическая конструкция, служащая для удвоения куба

Мы рассматривали до сих пор только проблемы геометрических построений без использования иных инструментов, кроме циркуля и линейки. Если допускаются и другие инструменты, то, разумеется, разнообразие возможных построений сильно увеличивается. Следующий пример может служить образцом того, как греки решали проблему удвоения куба. Рассмотрим (рис. 46) жесткий прямой угол MZN и подвижной прямоугольный крест VW,PQ. Двум дополнительным стержням RS и TU предоставлена возможность скользить, оставаясь перпендикулярными к сторонам прямого угла. На кресте пусть выбраны фиксированные точки Е и G, причем расстояния GB = a и BE = f заданы. Располагая крест таким образом, чтобы точки Е и G соответственно лежали на NZ и MZ, и перемещая стержни TU и RS, можно весь аппарат привести в такое положение, чтобы лучевые перекладины креста BW, BQ, BV проходили через вершины A, D, E прямоугольника ADEZ. Указанное на чертеже расположение всегда возможно при условии f >a. Мы видим сразу, что а:х = х:y = y:f, откуда, в частности, если положено f = 2а, получается х³ = 2а³. Значит, х есть ребро куба, объем которого вдвое больше, чем объем куба с ребром а. Таким образом, поставленная задача решена.

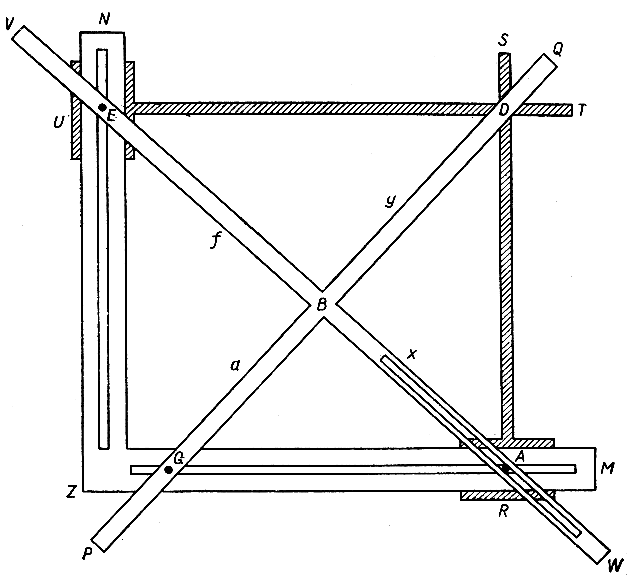
Рис. 46. Инструмент, служащий для удвоения куба