4. Как разделить отрезок пополам и как найти центр данной окружности с помощью одного циркуля

После того как мы научились находить точку, обратную данной, можно с помощью одного циркуля выполнить дальнейшие интересные построения. Например, сейчас мы найдем середину отрезка, концы которого А и В заданы, с помощью одного циркуля - не проводя самого отрезка. Вот решение этой задачи. Опишем окружность радиусом АВ с центром В и на ней, отправляясь от A, как раньше, отмерим последовательно три дуги радиусом AB. Последняя точка С будет лежать на прямой АВ, причем мы будем иметь: АВ = ВС. Затем опишем окружность радиуса АВ с центром А и построим точку С', обратную точке С относительно этой окружности. Тогда получим:

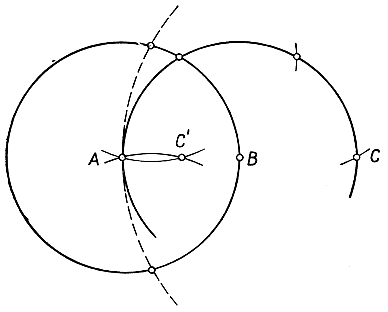
Рис. 44. Нахождение середины отрезка

Значит, С есть искомая середина отрезка.

Другое построение с помощью одного циркуля, также использующее обратные точки, заключается в нахождении центра данной окружности, когда начерчена только сама окружность, а центр не известен. Берем произвольную точку Р на окружности и около нее как центра описываем круг произвольного радиуса, пересекающийся с данным кругом в точках R и S. Из этих последних точек как центров описываем дуги радиусом RP = SP, пересекающиеся, кроме точки Р, еще в точке Q. Сравнивая то, что получилось, с рис. 41, мы видим, что неизвестный центр Q' есть точка, обратная точке Q относительно окружности с центром Р, и Q' может быть, как мы видели, построена с помощью одного циркуля.

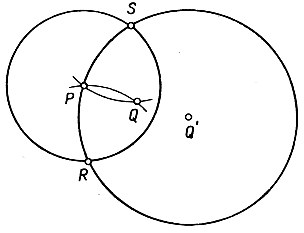
Рис. 45. Нахождение центра круга