3. Геометрическое построение обратных точек

Следующая теорема будет полезна в пункте 4 этого параграфа: точка Р', обратная данной точке Р относительно окружности С, может быть построена геометрически с помощью одного только циркуля. Рассмотрим сначала тот случай, когда точка Р находится вне круга С. Радиусом ОР опишем круговую дугу с центром Р, пересекающую С в точках R и S. Затем из этих точек как центров опишем круговые дуги радиусом r, равным радиусу круга С; эти дуги пересекутся в О и еще в точке Р' на прямой ОР. В равнобедренных треугольниках ORP и ORP'

так что треугольники подобны, и потому

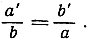
т. е.

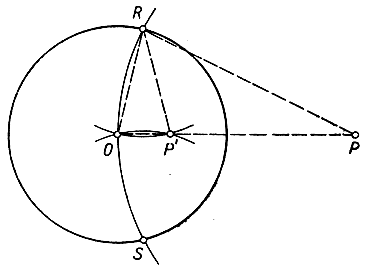
Рис. 41. Инверсия точки, внешней относительно окружности

Значит, Р' есть искомая точка, обратная точке Р.

Если данная точка Р лежит внутри С, то построение и доказательство остаются в силе, лишь бы окружность радиуса ОР с центром Р пересекала окружность С в двух точках. Если же пересечений не получается, то можно редуцировать построение к предыдущему случаю посредством следующего простого приема.

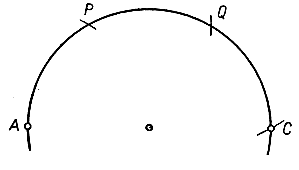
Рис. 42. Удвоение отрезка

Прежде всего заметим, что на прямой, соединяющей две данные точки A и О, можно с помощью одного циркуля построить такую точку С, что АО = ОС. Для этого достаточно провести окружность с центром О и радиусом r = АО. Затем начиная от точки А отметить последовательно на этой окружности такие точки Р, Q, С, что АР = PQ = QC = r. Тогда С есть как раз искомая точка: это ясно из того, что треугольники АОР, OPQ, OQC равносторонние, так что угол между ОА и ОС содержит 180° и ОС = OQ = АО. Повторяя указанную процедуру, мы имеем возможность отложить отрезок AO по прямой сколько угодно раз. Кстати, так как длина отрезка AQ равна r√3 (как читатель проверит без всякого труда), то нам удалось построить √3, исходя из единичного отрезка, не пользуясь линейкой.

Теперь мы можем построить точку, обратную точке Р относительно окружности С, как бы точка Р ни была расположена внутри С. Прежде всего на прямой ОР найдем такую точку R, что OR есть кратное ОР, и вместе с тем R лежит уже вне С:

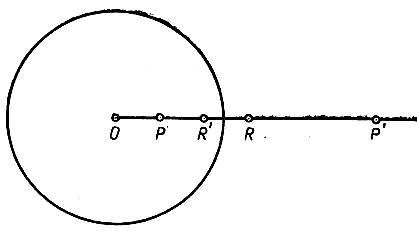
Рис. 43. Инверсия точки, внутренней относительно окружности

Для этого достаточно последовательно откладывать расстояние ОР посредством циркуля, пока мы не выберемся из круга С. Затем с помощью уже известного построения найдем точку R', обратную точке R. Тогда будем иметь:

Останется построить точку Р' по условию ОР' = n-OR', и задача будет решена.