2. Свойства инверсии

Самое важное свойство инверсии заключается в том, что она преобразует прямые линии и окружности в прямые линии и окружности. Точнее, мы сейчас обнаружим, что в результате инверсии:

a) прямая, проходящая через О, становится прямой, проходящей через О,

b) прямая, не проходящая через О, становится окружностью, проходящей через О,

c) окружность, проходящая через О, становится прямой, не проходящей через О,

d) окружность, не проходящая через О, становится окружностью, не проходящей через О.

Утверждение а) не требует доказательства, так как из самого определения инверсии ясно, что каждая точка на рассматриваемой прямой имеет в качестве образа другую точку на той же прямой, так что хотя отдельные точки на прямой перемещаются, но прямая в целом остается неизменной.

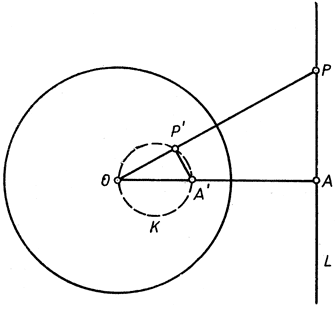
Рис. 39. Инверсия прямой относительно окружности

Докажем утверждение b). Из О опустим перпендикуляр на данную прямую L (рис. 39). Пусть А - основание этого перпендикуляра, А' - точка, обратная точке А. Возьмем произвольную точку Р на L и обозначим через Р' точку, ей обратную. Так как ОА*ОА' = ОР*ОР' = r², то отсюда следует, что

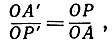
поэтому треугольники ОР'А' и ОАР подобны и, значит, угол ОР'А' прямой. В таком случае из теорем элементарной геометрии вытекает, что Р' лежит на окружности К с диаметром 0А'; эта окружность и является, следовательно, образом прямой L. Итак, утверждение b) доказано. Утверждение с) следует из того, что если образ L есть K, то образ К есть L.

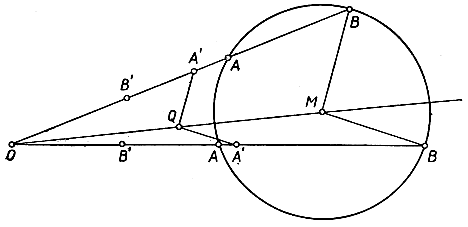
Рис. 40. Инверсия окружности

Остается доказать утверждение d). Пусть К - окружность, не проходящая через О, с центром М и радиусом k (рис. 40). Чтобы получить ее образ, проведем через О прямую, пересекающую К в точках А и В, и затем посмотрим, как изменяются образы А' и B', когда направление прямой изменяется и она пересекает K самыми разнообразными способами. Обозначим расстояния ОА, ОB, ОА', ОВ', ОМ через а, b, а', b', m, и пусть t есть длина касательной к K, проведенной из точки О. По определению инверсии мы имеем аа' = bb' = r², а по элементарно геометрическому свойству окружность аb = t². Если разделим первые равенства на второе, то получим:

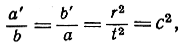
где с² зависит только от r и t и, значит, не зависит от положения точек А и В. Теперь проведем через А' прямую, параллельную ВМ; пусть Q есть точка ее пересечения с ОМ. Положим OQ = q, A'Q = ρ. Тогда

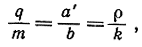
или же

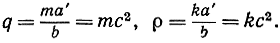
Это означает, что при всевозможных положениях А и В точка Q на прямой ОМ всегда будет одна и та же и что расстояние А'Q также не будет меняться. Точно так же В'Q = ρ, так как 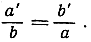Итак, образами точек А и В на K будут точки, расстояния которых от Q равны постоянной величине ρ, т. е. образ К есть окружность. Утверждение d) доказано.