1. Общие замечания

В настоящей, второй части этой главы мы систематически рассмотрим некоторые общие принципы, которые могут быть приложены к конструктивным проблемам. Многие из этих проблем обозреваются гораздо легче, если смотреть на них с общей точки зрения "геометрических преобразований". Вместо того чтобы изучать отдельное построение, мы займемся сразу целым классом проблем, связанных между собой теми или иными процедурами преобразований. Способность бросать яркий свет на существо вещей, присущая идее класса геометрических преобразований, никоим образом не ограничена конструктивными проблемами, но имеет ближайшее отношение ко всей геометрии в целом. В главах IV и V мы будем иметь случай оценить роль геометрических преобразований в этом более широком аспекте. Пока же мы подвергнем изучению один из частных типов преобразований - инверсию плоскости относительно окружности, представляющую собой обобщение обыкновенного зеркального отражения относительно прямой линии.

Говоря о преобразовании (отображении) плоскости самой в себя, мы имеем в виду некоторое правило, сопоставляющее каждой точке Р плоскости некоторую другую точку Р' той же плоскости. Точка Р' называется образом точки Р, точка Р - прообразом точки Р'. Простейший пример такого преобразования - зеркальное отражение (осевая симметрия) плоскости относительно данной прямой линии L: точка Р по одну сторону L имеет своим образом точку Р', расположенную по другую сторону L таким образом, что L является перпендикуляром к отрезку РР', восставленным из его середины. Преобразование может оставлять некоторые точки плоскости неподвижными; в нашем примере таковы точки самой прямой L.

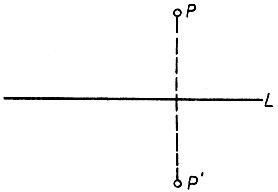
Рис. 37. Отражение точки относительно прямой

Дальнейшими примерами преобразований являются вращения плоскости относительно неподвижной точки О, затем параллельные переносы, перемещающие каждую точку в данном направлении на одно и то же расстояние (эти преобразования не имеют неподвижных точек), и, наконец, в качестве несколько более общего примера следует назвать движения плоскости, которые можно представлять себе составленными из вращений и параллельных перенесений.

Но в данный момент нас интересует иной, частный класс преобразований - именно инверсии относительно окружностей. (Иногда их называют круговыми отражениями, имея ввиду сходство этого преобразования с отражением в сферическом зеркале.) Пусть в неподвижной плоскости задана некоторая окружность С с центром О (называемым центром (или полюсом) инверсии) и радиусом r. Образ точки Р определяется как точка Р', лежащая на прямой OP по ту же сторону от О, что и Р, и такая, что

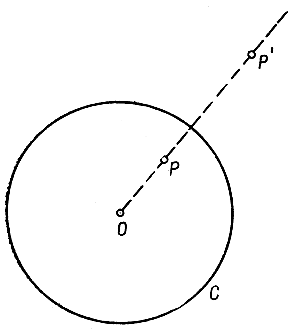
Рис. 38. Инверсия точки относительно окружности

Из этого определения следует, что если Р' есть образ Р, то и Р есть (в данном преобразовании) образ Р'. Это дает право называть точки Р и Р' взаимно обратными относительно окружности С. Инверсия превращает внутреннюю область окружности во внешнюю, и обратно: в самом деле, из неравенства ОР<r следует неравенство ОР'>r и, напротив, из неравенства ОР>r - неравенство ОР'<r. Неподвижными точками плоскости являются точки самой окружности С.

Правило (1) не определяет никакого образа для центра (полюса) О. Но ясно, что, когда движущаяся точка Р приближается к О, ее образ Р' уходит неограниченно далеко. По этой причине иногда говорят, что при инверсии образом центра является бесконечно удаленная точка. Полезность этой терминологии вытекает из того обстоятельства, что она дает нам право утверждать, что инверсия устанавливает взаимно однозначное соответствие между всеми точками плоскости без исключения и их образами: каждая точка плоскости имеет один и только один образ и сама является образом одной и только одной точки. Отметим, что это последнее свойство принадлежит также и раньше приведенным примерам геометрических преобразований.