3. Повторные отражения

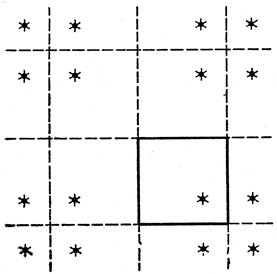
Рис. 65. Повторное отражение относительно прямолинейных стен

Каждому из нас приходилось наблюдать странные явления отражения, возникающие, если имеется более одного зеркала. Если четыре стены прямоугольной комнаты представляют собой идеальные зеркала, ни в малой степени не поглощающие света, то освещенная, находящаяся в этой комнате точка создает бесконечное множество отражений, по одному на каждую из конгруэнтных прямоугольных комнат, возникающих из первой посредством отражений (рис. 65). При менее правильной форме соединения зеркал, например при трех зеркалах, создается более сложная система отражений. Получающуюся конфигурацию легко описать только в том случае, если отраженные треугольники, не перекрывая друг друга взаимно, полностью покрывают плоскость. Таким свойством обладают только прямоугольный равнобедренный треугольник, равносторонний треугольник и прямоугольный треугольник, представляющий собой половину равностороннего (рис. 66).

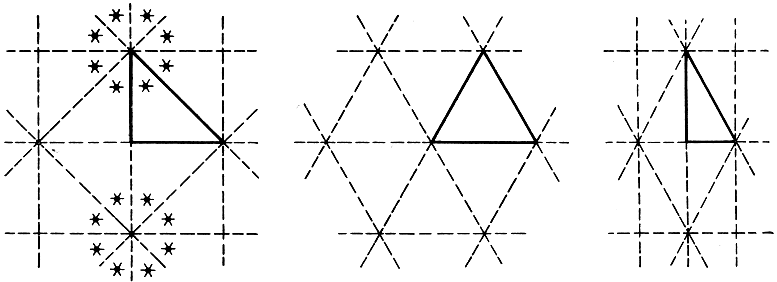
Рис. 66. Правильные системы треугольных зеркал

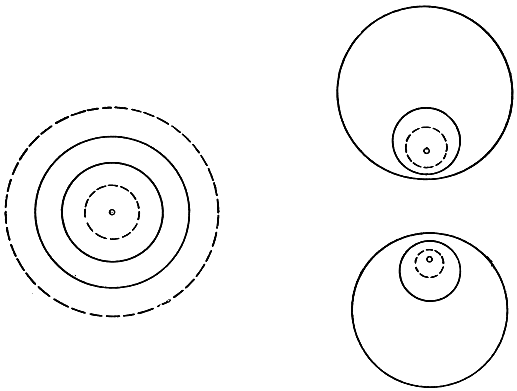
Рис. 67. Повторное отражение относительно двух сферических зеркал

Еще более курьезные обстоятельства возникают, если мы станем рассматривать повторные инверсии относительно пары окружностей. Поместившись между двумя концентрическими сферическими зеркалами, мы увидали бы бесчисленное множество концентрических отражений. Одна последовательность отражений уходила бы в бесконечность, другая - сосредоточивалась бы около центра. Случай двух окружностей, расположенных одна вне другой, несколько сложнее: окружности и их отражения последовательно отражаются одна в другой, уменьшаясь после каждого отражения и теснясь к двум предельным точкам, по одной в каждой из данных окружностей. (Эти точки обладают свойством взаимной обратности относительно каждой из данных окружностей.) Все это показано на рис. 67. Что получится в случае трех окружностей, об этом читатель может составить впечатление, взглянув на узор, изображенный на рис. 68.

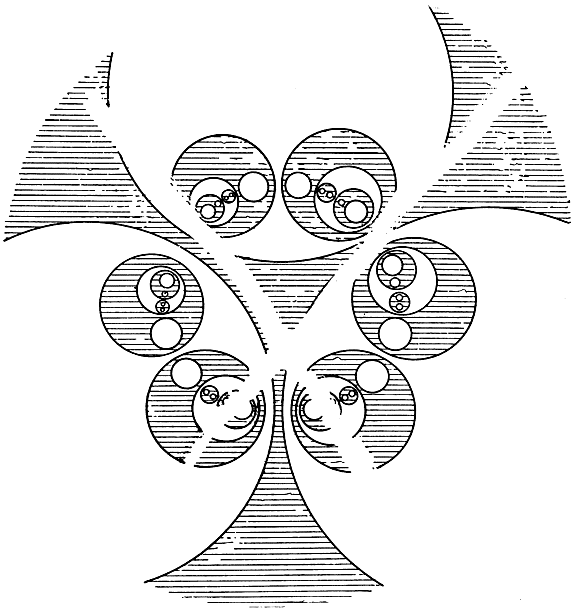
Рис. 68. Отражение относительно трех сферических зеркал