4. Правильный семиугольник

Перейдем теперь к проблеме построения стороны х правильного семиугольника, вписанного в единичный круг. Проще всего справиться с этой проблемой, если прибегнуть к комплексным числам (см. главу II, § 5) Мы знаем, что вершины правильного семиугольника служат корнями уравнения

причем координаты х, y каждой вершины являются действительной и мнимой частями комплексного числа z = х + iy. Один из корней есть z = 1, а остальные удовлетворяют уравнению

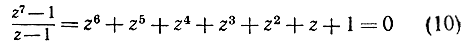
(10)

(см. стр. 127). Деля на 23, получаем новое уравнение

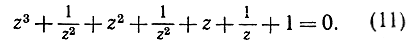
(11)

Простые алгебраические преобразования приводят его к виду

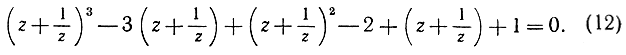
(12)

Положив теперь

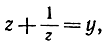
мы приходим окончательно к уравнению третьей степени

Мы знаем, что z, корень седьмой степени из единицы, дается формулой

где 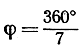есть угол, под которым из центра круга видна сторона семиугольника; кроме того, из упражнения 2 на стр. 128 следует, что 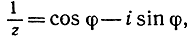так что

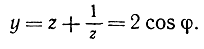
Если мы сумеем построить y, то сумеем построить и cos φ, и обратно. Итак, раз будет установлено, что величина y не может быть построена, то тем самым будет установлено, что не могут быть построены ни величина cos φ, ни величина z; следовательно, невозможно будет построение семиугольника.

Таким образом, в силу теоремы пункта 2, остается показать, что уравнение (13) не имеет рациональных корней. Это тоже доказывается косвенным методом. Допустим, что уравнение (13) имеет рациональный корень 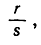где r и s - целые числа без общих множителей. В таком случае должно удовлетворяться равенство

отсюда ясно, что r³ делится на s, a s³ - на r. Так как r и s - взаимно простые числа, то отсюда следует, что каждое из них равно ±1. Значит, и y, если только это число рациональное, должен равняться или +1, или -1. Но подстановка в уравнение (13) показывает, что ни +1, ни -1 не являются корнями уравнения. Итак, нельзя построить величины y, а следовательно, и стороны семиугольника.