
3. Трисекция угла
Покажем, что трисекция угла с помощью только циркуля и линейки в общем случае невозможна. Конечно, существуют углы, например, углы в 90° или в 180°, для которых трисекция выполняется. Но мы должны показать, что не существует процедуры построения, пригодной для всякого угла. Так как общий метод должен был бы относиться ко всем углам, то наша цель будет достигнута, если мы укажем хотя бы один какой-нибудь угол, для которого трисекция невозможна. Итак, несуществование общего метода трисекции будет установлено, если мы убедимся, что, например, угол в 60° не может быть разделен на три равные части с помощью только циркуля и линейки.
Алгебраический эквивалент рассматриваемой проблемы можно получить разными способами; самый простой способ - считать, что угол θ задан своим косинусом: cos θ = g. Тогда проблема сводится к вычислению величины x = cos θ/3. Интересующие нас косинусы связаны между собой простой тригонометрической формулой (см. стр. 125)
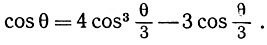
Другими словами, проблема трисекции угла θ (такого, что cos θ = g) равносильна построению корня кубического уравнения
4z3 - 3z - g = 0. (6)
Так как по предыдущему мы имеем право положить 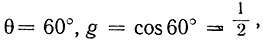 то уравнение (6) принимает вид
то уравнение (6) принимает вид
8z3 - 6z = 1. (7)
В силу теоремы, доказанной в предыдущем пункте, для нашей цели достаточно показать, что это уравнение не имеет рациональных корней. Положим v = 2z; уравнение примет еще более простой вид
v3 - 3v = 1. (8)
Если бы существовало рациональное число 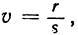 удовлетворяющее этому уравнению, где r и s - целые числа без общего множителя (>1), то мы должны были бы иметь равенство r3 - 3s2r = s3. Отсюда следовало бы, что число s3 - r(r2 - 3s2) делится на r, и тогда получилось бы, что r и s имеют общий множитель, если только r не равно +1. Совершенно так же мы заключили бы, что число r3 = s2(s + 3r) делится на s2, а это значило бы, что r и s имеют общий множитель, если только s не равно ± 1. Но так как дробь r/s по предположению несократима, то, значит, остается заключить, что числа r и s равны ±1, т. е. v = ±1. Но, подставляя v = +1 и v = -1 в уравнение (8), мы видим, что в обоих случаях уравнение не удовлетворяется. Итак, уравнение (8), а следовательно, и уравнение (7) не имеют рациональных корней; тем самым невозможность трисекции угла доказана.
удовлетворяющее этому уравнению, где r и s - целые числа без общего множителя (>1), то мы должны были бы иметь равенство r3 - 3s2r = s3. Отсюда следовало бы, что число s3 - r(r2 - 3s2) делится на r, и тогда получилось бы, что r и s имеют общий множитель, если только r не равно +1. Совершенно так же мы заключили бы, что число r3 = s2(s + 3r) делится на s2, а это значило бы, что r и s имеют общий множитель, если только s не равно ± 1. Но так как дробь r/s по предположению несократима, то, значит, остается заключить, что числа r и s равны ±1, т. е. v = ±1. Но, подставляя v = +1 и v = -1 в уравнение (8), мы видим, что в обоих случаях уравнение не удовлетворяется. Итак, уравнение (8), а следовательно, и уравнение (7) не имеют рациональных корней; тем самым невозможность трисекции угла доказана.
Эта теорема доказана в предположении, что линейка рассматривается как инструмент, служащий для проведения прямой через две данные точки, и никак иначе. В самом деле, когда мы давали общую характеристику чисел, которые допускают построение, имелось в виду только такое употребление линейки. Если допустить иные приемы пользования линейкой, то совокупность выполненных построений чрезвычайно расширяется. Хорошим примером является следующий метод трисекции угла, указываемый в сочинениях Архимеда.
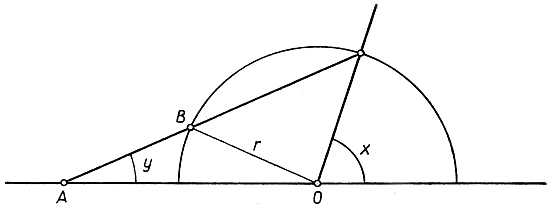
Рис. 36. Метод трисекции угла, указанный Архимедом
Пусть дан угол х (рис. 36). Продолжим горизонтальную сторону угла влево и затем проведем полукруг с центром О и произвольным радиусом r. Отметим на самой линейке такие точки А и В, что АВ = r. Затем приведем линейку в такое положение, чтобы точка А линейки была на продолженной стороне угла, точка В на проведенном полукруге и вместе с тем линейка прошла бы через точку пересечения второй стороны угла с полукругом. В этом положении линейки проведем по ней прямую линию, образующую с продолженной стороной данного угла угол, который обозначим через y.
Упражнение. Доказать, что 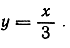
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'