§ 3. Неразрешимость трех классических проблем

1. Удвоение куба

Теперь мы уже достаточно подготовлены к исследованию известных еще с древности проблем трисекции угла, удвоения куба и построения правильного семиугольника. Рассмотрим прежде всего задачу об удвоении куба.

Если данный куб имеет ребро, равное единице, его объем будет равен кубической единице; требуется найти ребро х куба, объем которого вдвое больше. Итак, искомое ребро удовлетворяет простому кубическому уравнению

Наше доказательство невозможности построения числа х с помощью только циркуля и линейки будет носить "косвенный" характер. Допустим, что такое построение возможно. Тогда согласно полученным выше результатам число х должно принадлежать некоторому полю F_k, полученному так, как было объяснено раньше,- из рационального поля посредством последовательного "присоединения" квадратных корней. Мы сейчас убедимся в том, что такое допущение приведет к противоречию.

Мы уже знаем, что число х не может принадлежать рациональному полю F₀, так как 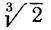есть число иррациональное (см. упражнение 1 на стр. 186). Значит, придется допустить, что оно принадлежит одному из расширенных полей F_k, где k - целое положительное число. Мы имеем право допустить, что k есть наименьшее из таких целых чисел, т. е. что х принадлежит F_k, но не принадлежит F_k-1. Это значит, что х имеет вид

где р, q и ω принадлежат какому-то полю F_k-1, но √ω ему не принадлежит. Основываясь, далее, на довольно простом алгебраическом рассуждении (подобные рассуждения приходится применять нередко), мы убедимся, что если p + q√ω есть решение уравнения (1), то y = р - q√ω есть также его решение. Так как х принадлежит полю F_k, то х³ и х³-2 тоже принадлежат F_k и, значит,

где а и b принадлежат F_k-1. Нетрудно подсчитать, что а = р³ + 3pq²ω - 2, b = 3p²q + q³ω. Если положим

то сразу видно, что

Так как мы предположили, что х есть корень уравнения (1), то

Но из последнего равенства следует (это основной момент рассуждения!), что оба числа а и b равны нулю. Действительно, если бы b было отлично от нуля, то из (3) получилось бы равенство а это противоречит допущению, что √ω не принадлежит полю F_k-1. Итак, b = 0, и тогда из (3) следует, что а = 0.

Но раз мы установили, что а = b = 0, то уже из равенства (2') немедленно вытекает, что y = р - q√ω есть решение уравнения (1), так как у³ - 2 = 0. Далее, y≠х, т. е. х - y ≠0, так как число х - у = 2q√ω могло бы обращаться в нуль только при q = 0, а в этом случае х = р принадлежало бы полю F_k-1, чего мы не предполагали.

Мы установили, что если х = р + q√ω есть корень кубического уравнения (1), то y = р - q√ω есть другой, не равный ему корень того же уравнения. Но это немедленно приводит к противоречию: y = р - q√ω есть, очевидно, действительное число, так как числа р, q, √ω действительные, уравнение же (1) имеет только один действительный корень, а два - мнимых (см. стр. 126).

Наше первоначальное допущение привело к противоречию, значит, оно ошибочно; поэтому корень уравнения (1) не может принадлежать никакому полю F_k. Итак, удвоение куба с помощью только циркуля и линейки невозможно.