2. Все числа, допускающие построение,- алгебраические

Если начальное поле F₀ есть рациональное поле (порождаемое единственным отрезком), то все числа, допускающие построение, принадлежат к числу алгебраических. (Определение алгебраических чисел было дано на стр. 131.) Именно числа поля F₁ являются корнями квадратных уравнений, числа поля F₂ - корнями уравнений четвертой степени и вообще числа поля F_k - корнями уравнений степени 2^k с рациональными коэффициентами. Докажем это сначала для поля F₂, причем начнем с примера. Пусть

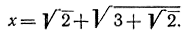
Мы получаем (х - √2)² = 3 + √2, х² + 2 - 2√2х = 3 + √2, или х² - 1 = √2 (2х + 1) - квадратное уравнение с коэффициентами из F₁. Возведение в квадрат приводит к уравнению

четвертой степени с рациональными коэффициентами. В общем случае любое число поля F₂ имеет вид

где р, q, ω принадлежат полю F₁ и, значит, имеют вид р = а + b√s , q = c + d√s , ω = e + f√s, где a, b, c, d, e, f, s - рациональные числа. Из равенства (4) мы получаем

причем все коэффициенты принадлежат полю F₁, порождаемому величиной √s. Поэтому последнее равенство можно переписать в виде

где коэффициенты r, s, t, u, v - рациональные. Возводя в квадрат, получим уравнение четвертой степени

с рациональными коэффициентами, как и требовалось.

Упражнения. 1) Построить уравнение с рациональными коэффициентами для чисел:

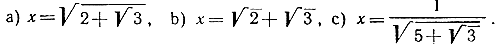
2) Построить таким же образом уравнение восьмой степени для чисел:

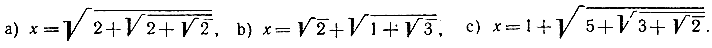
Чтобы закончить доказательство теоремы в общем случае, когда х принадлежит полю F_k с произвольным индексом k, достаточно установить, как выше, что х удовлетворяет квадратному уравнению с коэффициентами из поля F_k-1. Затем, повторяя процедуру доказательства, убеждаемся, что х удовлетворяет уравнению степени 2² = 4 с коэффициентами из поля F_k-2 и т. д.

Упражнение. Закончите это общее доказательство, применяя метод математической индукции: докажите, что х удовлетворяет уравнению степени 2^l с коэффициентами из поля F_k-l, 0<l≤k. При l =k получается окончательный результат.