3. Проблема Аполлония

Другая конструктивная проблема, решающаяся весьма просто, если подойти к ней с алгебраической точки зрения,- это знаменитая и уже упомянутая выше проблема Аполлония о проведении окружности, касательной к трем данным окружностям. В настоящем контексте нам не представляется необходимым искать ее особенно элегантное решение. Нам существенно лишь установить принципиально важное положение: проблема Аполлония решается с помощью циркуля и линейки. Мы вкратце приведем соответствующее доказательство; вопрос же о наиболее элегантном построении будет разобран ниже (см. стр. 191 - 192).

Пусть центры трех данных кругов имеют соответственно координаты (x₁, y₁), (x₂, y₂) и (x₃, y₃), а радиусы равны r₁, r₂ и r₃. Обозначим координаты центра искомого круга через (х, y), а радиус через r. Легко написать условие касания двух окружностей, если учесть, что расстояние между центрами должно равняться сумме или разности радиусов, смотря по тому, имеет ли место внешнее или внутреннее касание. Записывая в алгебраической форме три условия задачи, мы получаем три уравнения:

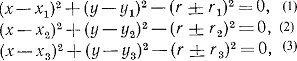
которые после преобразований принимают вид

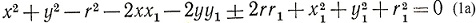
и т. п.

В каждом из уравнений нужно брать знак плюс или минус, в зависимости от того, каково касание - внешнее или внутреннее (рис. 35). Уравнения (1), (2), (3) - второй степени относительно неизвестных х, y, r, но они обладают тем свойством, что члены второй степени входят в одинаковой комбинации, как видно из развернутой формы (1а). Таким образом, вычитая (2) из (1), мы получаем уравнение, линейное относительно х, y, r:

где а = 2(х₂ - x₁), и т. д. Точно так же, вычитая (3) из (1), будем иметь другое линейное уравнение:

Решая уравнения (4) и (5) относительно неизвестных х и y, которые, таким образом, выразятся линейно через r, а затем подставляя в (1), придем к уравнению, квадратному относительно r, каковое может быть решено с помощью рациональных операций и извлечения корня (см. стр. 151). Это уравнение, вообще говоря, будет иметь два решения, из которых лишь одно будет положительным. Определив r, найдем дальше значения х и y, подставляя r в ранее полученные формулы. Окружность с центром х, y и радиусом r и должна быть касательной к трем данным окружностям. Во всей процедуре решения участвуют только рациональные операции и извлечение квадратного корня. Отсюда следует, что построение х, y и r может быть выполнено с помощью только циркуля и линейки.

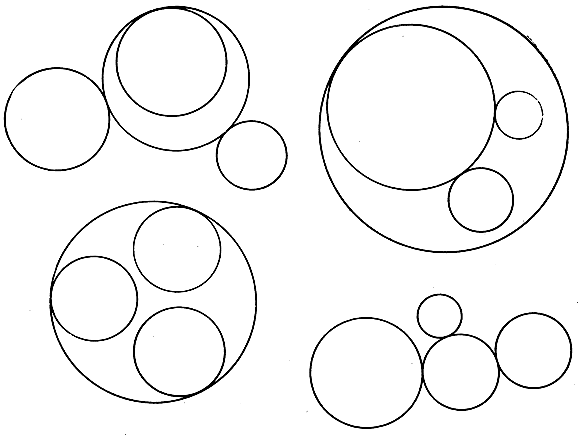
Рис. 35. Круги Аполлония

В общем случае будет иметься 8 решений проблемы Аполлония в соответствии с возможными 2*2*2 = 8 комбинациями в выборе знаков + и - в уравнениях (1), (2) и (3); выбор же знаков надлежит делать в зависимости от того, какого рода касание - внешнее или внутреннее - желательно иметь по отношению к каждому из данных кругов. Вполне возможно, что наша алгебраическая процедура не приведет к действительным значениям х, y и r. Таков будет, например, случай, когда все три данных круга - концентрические; тогда, очевидно, наша геометрическая задача не будет иметь ни одного решения. Следует также предвидеть возможность и случаев "вырождения": например, если все три окружности "вырождаются" в точки, лежащие на одной прямой; тогда аполлониева окружность тоже "вырождается" в эту самую прямую. Мы не видим необходимости рассматривать вопрос во всех подробностях: это сделает сам читатель, если он обладает некоторыми алгебраическими навыками.