2. Правильные многоугольники

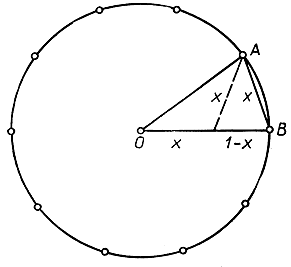
Рис. 32. Правильный десятиугольник

Рассмотрим теперь несколько более сложные конструктивные задачи. Начнем с построения правильного десятиугольника. Предположим, что правильный десятиугольник вписан в круг радиуса 1 (рис. 32); обозначим его сторону через х. Так как центральный угол, под которым эта сторона х видна из центра круга, содержит 36°, то остальные два угла большого треугольника содержат каждый по 72°, и, значит, пунктирная линия, делящая пополам угол A, разбивает треугольник ОАВ на два равнобедренных треугольника с равными боковыми сторонами длины х. Радиус круга, таким образом, составляется из отрезков х и 1-х. Так как треугольник ОАВ подобен меньшему из двух треугольников, на которые он разбивается, то мы получаем 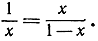Эта пропорция приводит к квадратному уравнению х² + х - 1 = 0, решение которого имеет вид 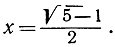(Другое решение нас не интересует, так как оно соответствует отрицательному значению х.) Из полученной формулы ясно, что отрезок х может быть построен геометрически. Имея же отрезок х, мы сможем построить правильный десятиугольник, откладывая по окружности десять раз хорду х. Отсюда уже легко получить и правильный пятиугольник, соединяя вершины десятиугольника через одну.

Вместо того чтобы строить √5 тем методом, который указан на рис. 31, мы можем также построить гипотенузу прямоугольного треугольника со сторонами 1 и 2. Затем придется отнять единичный отрезок и то, что получится, разделить пополам.

Отношение 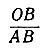в рассмотренной задаче было названо "золотым", так как, по мнению греческих математиков, прямоугольник, стороны которого находятся в этом отношении, эстетически особенно приятен для глаза. Значение отношения приблизительно равно 1,62.

Из всех правильных многоугольников легче всего построить шестиугольник. Так как длина стороны такого шестиугольника, вписанного в круг, равна радиусу круга, то сам шестиугольник строится без затруднений, если отложим шесть раз по окружности отрезок, равный радиусу.

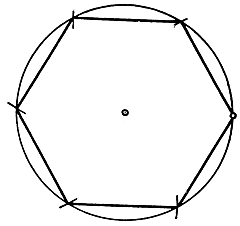
Рис. 33. Правильный шестиугольник

Имея правильный n-угольник, можно сразу же получить и правильный 2n-угольник, деля пополам дуги между соседними вершинами n-угольника. Начиная с диаметра круга (правильного вписанного "двуугольника"), мы построим последовательно 4, 8, 16, ..., 2ⁿ-угольники. Таким же образом, начиная с шестиугольника, мы получим 12, 24, 48, ... -угольники, а начиная с "десятиугольника,- 20, 40, ... -угольники.

Если s_n обозначает длину стороны правильного n-угольника, вписанного в единичный круг (т. е. круг с радиусом 1), то сторона правильного вписанного 2n-угольника будет иметь длину

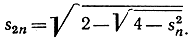
Доказывается это следующим образом (рис. 34): s_n = DE = 2DC, s_2n = DB и АВ = 2. Площадь прямоугольного треугольника ABD равна 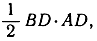или, с другой стороны, 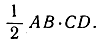Так как 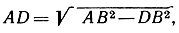то, подставляя 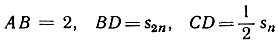и сравнивая между собой два выражения для площади, мы получаем:

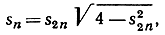
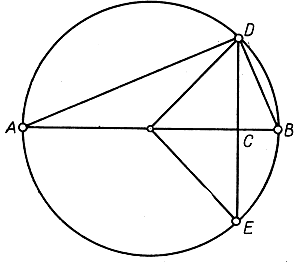
Рис. 34. Удвоение числа сторон правильного многоугольника

Остается решить квадратное уравнение относительно х = s²_2n и при выборе корня принять во внимание, что х должно быть меньше 2.

Из этой формулы, так как длина S₄ (сторона квадрата) равна √2, следует, что

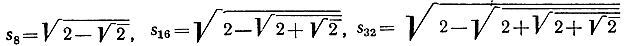
и т. д.

В качестве общей формулы мы получаем (при n>2):

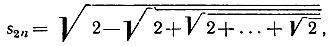
причем в правой части должно быть всего n-1 радикалов. Периметр 2n-угольника, вписанного в круг радиуса 1, равен 2ⁿs_2n. Когда n стремится к бесконечности, этот периметр в пределе переходит в длину окружности, по определению равную 2π:

2ⁿs_2n→2π при n→∞.

Деля на два и подставляя m вместо n-1, мы получаем следующую формулу для π:

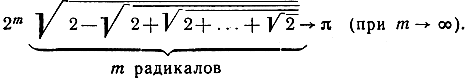
Упражнение. Пользуясь тем, что 2^m→∞, доказать, как следствие, что

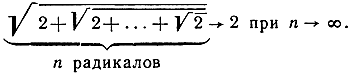
Резюмируем полученные здесь результаты таким образом: стороны правильных, вписанных в единичный круг 2n-угольников, 5*2n-угольников и 3*2n-угольников вычисляются посредством рациональных операций - сложения, вычитания, умножения, деления - и операции извлечения квадратного корня; следовательно, они могут быть построены с помощью только циркуля и линейки.