
1. Построение полей и извлечение квадратных корней
В порядке развития общих идей мы начнем с рассмотрения небольшого числа классических построений. Более углубленное изучение возможности геометрических построений неизбежно связано с переводом геометрической задачи на язык алгебры. Всякая проблема геометрического построения может быть схематизирована следующим образом: дано некоторое число отрезков, скажем, а, b, с, ...; требуется построить один или несколько отрезков х, y, ... . Даже если на первый взгляд проблема как будто имеет совсем иной вид, ее всегда можно переформулировать таким образом, чтобы она включилась в указанную схему. Искомые отрезки фигурируют или в виде сторон треугольника, который требуется построить, или в виде радиусов кругов, или как прямоугольные координаты каких-то искомых точек (см., например, стр. 153). Предположим для простоты, что требуется построить какой-то отрезок х. В таком случае геометрическое построение приводит к решению алгебраической задачи: установить соотношение (в форме уравнения) между искомой величиной х и данными величинами а, b, с, ...; затем, решая это уравнение, найти формулу для величины х и, наконец, выяснить, можно ли свести вычисление х к таким алгебраическим процедурам, которые соответствуют построениям, выполнимым с помощью циркуля и линейки. Таким образом, в основе всей рассматриваемой теории лежит принцип аналитической геометрии - количественная характеристика геометрических объектов, основанная на введении континуума действительных чисел.
Заметим прежде всего, что простейшие алгебраические операции соответствуют элементарным геометрическим построениям. Если даны два отрезка, длины которых равны а и b (измерение производится посредством "единичного" отрезка), то очень легко построить отрезки а + b, а - b, ra (где r - рациональное число), a/b и аb.
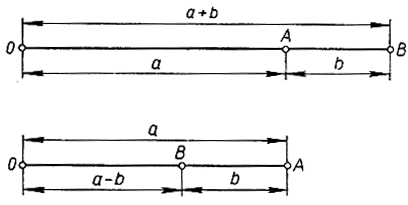
Рис. 27. Построение a+b и a-b
Чтобы построить а + b (рис. 27), мы проводим прямую линию и на ней откладываем циркулем отрезки ОА = а и АВ = b. Тогда ОВ = а + b. Точно так же в случае а - b мы откладываем О А = а и А В = b, но на этот раз откладываем b в сторону, противоположную той, в которую отложили а. Тогда ОВ = а - b. Чтобы построить За, мы просто строим а + а + а; аналогично поступаем, если нужно построить ра, где р - целое число, у строится следующим приемом (рис. 28): на произвольной прямой откладываем ОА = а и затем проводим другую прямую через точку О. На этой прямой откладываем произвольный отрезок ОС = с и строим OD = 3c. Соединяем А и D прямой линией и проводим через точку С прямую, параллельную AD; пусть эта прямая пересекает ОА в точке В. Треугольники ОВС и OAD подобны; значит, 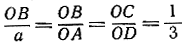 и OB =
и OB = 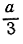 Так же образом можно вообще построить
Так же образом можно вообще построить 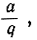 где q - целое. Совершая эту операцию над отрезком ра, мы построим rа, где
где q - целое. Совершая эту операцию над отрезком ра, мы построим rа, где 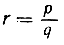 какое угодно рациональное число.
какое угодно рациональное число.
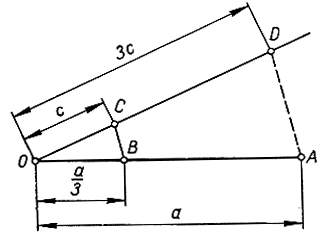
Рис. 28. Построение
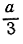
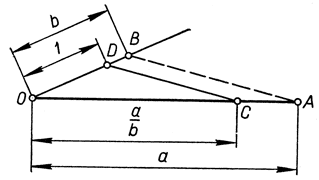
Рис. 29. Построение a/b
Чтобы построить a/b (рис. 29), откладываем OB = b и ОА = а на сторонах произвольного угла с вершиной О и на стороне ОБ откладываем отрезок OD = 1. Через D проводим прямую, параллельную АВ; пусть она пересекает ОА в точке С. Тогда будем иметь: 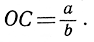 Построение аb показано на рис. 30; здесь AD - прямая, проходящая через А и параллельная ВС.
Построение аb показано на рис. 30; здесь AD - прямая, проходящая через А и параллельная ВС.
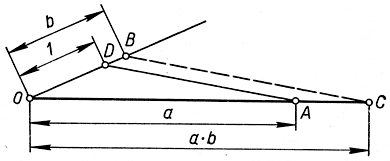
Рис. 30. Построение ab
Из этих соображений вытекает, что "рациональные"алгебраические операции - сложение, вычитание, умножение и деление,- производимые над заданными величинами, могут быть выполнены посредством геометрических построений. Исходя из данных отрезков, измеряемых действительными числами а, b, с, ..., мы можем, последовательно выполняя эти простые построения, построить любую величину, которая через а, b, с, ... выражается рационально, т. е. с помощью лишь перечисленных выше четырех основных действий. Совокупность всех величин, которые таким образом могут быть получены из а, b, с, ..., образует то, что называется числовым полем - множество чисел, обладающее тем свойством, что любая рациональная операция, совершенная над двумя (или более) элементами этого множества, приводит снова к элементу этого же множества. Мы напоминаем, что совокупность всех рациональных чисел, совокупность всех действительных чисел, совокупность всех комплексных чисел образуют такие поля. В рассматриваемом нами теперь случае говорят, что поле порождается данными числами а, b, с, ... .
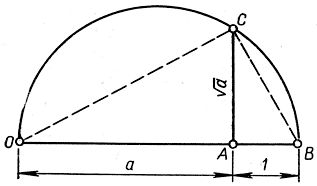
Рис. 31. Построение √a
Существенно новой операцией, выводящей нас за пределы полученного поля, является извлечение квадратного корня. Если задан отрезок а, то отрезок √a может быть построен с помощью только циркуля и линейки. На произвольной прямой мы откладываем ОА = а и АВ = 1 (рис. 31). Проводим, далее, окружность диаметром ОВ и из точки А восставляем перпендикуляр к ОБ; пусть он пересекает* окружность в точке С. Угол С в треугольнике ОВС - прямой (по известной теореме элементарной геометрии: угол, вписанный в полуокружность,- прямой). Значит, ∠OCA = ∠АВС, прямоугольные треугольники ОАС и CAB подобны, и, полагая АС = х, мы получаем:
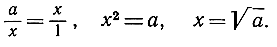
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'