2. Применение к математической логике

Проверка законов алгебры множеств основывалась на анализе логического смысла соотношения А⊂В и операций A + В, АВ и А'. Мы можем теперь обратить этот процесс и рассматривать законы 1)-26) как базу для "алгебры логики". Скажем точнее: та часть логики, которая касается множеств, или, что по существу то же, свойств рассматриваемых объектов, может быть сведена к формальной алгебраической системе, основанной на законах 1)-26).

Логическая "условная вселенная" определяет множество I; каждое свойство И определяет множество А, состоящее из тех объектов в I, которые обладают этим свойством. Правила перевода обычной логической терминологии на язык множеств ясны из следующих примеров:

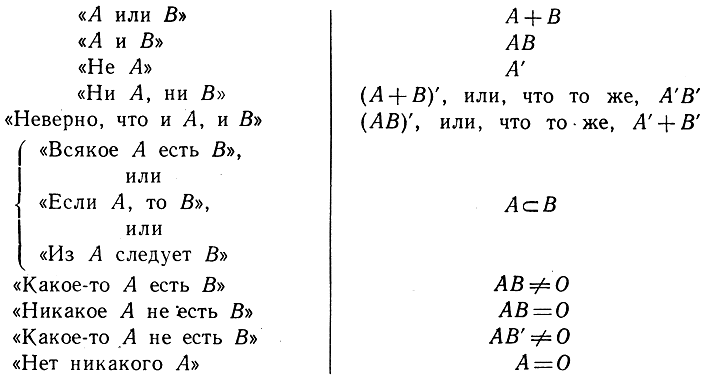
В терминах алгебры множеств силлогизм "Barbara", обозначающий, что "если всякое Л есть В и всякое В есть С, то всякое Л есть С", принимает простой вид:

3) Если A⊂В и В⊂С, то A⊂С.

Аналогично "закон противоречия", утверждающий, что "объект не может одновременно обладать и не обладать некоторым свойством", записывается в виде

20) АА' = О,

а "закон исключенного третьего", говорящий, что "всякий объект либо обладает, либо не обладает данным свойством", в виде

19) А + А' = I.

Таким образом, та часть логики, которая выразима в терминах символов ⊂, +, * и ', может трактоваться как формальная алгебраическая система, подчиненная законам 1)-26). На основе слияния логического анализа математики и математического анализа логики создалась новая дисциплина - математическая логика, которая в настоящее время находится в процессе бурного развития.

С аксиоматической точки зрения заслуживает внимания тот замечательный факт, что утверждения 1)-26); вместе со всеми прочими теоремами алгебры множеств, могут быть логически выведены из следующих трех равенств:

Отсюда следует, что алгебра множеств может быть построена как чисто дедуктивная теория, вроде евклидовой геометрии, на базе этих трех положений, принимаемых в качестве аксиом. Если эти аксиомы приняты, то операция АВ и отношение А⊂В определяются в терминах A + В и А':

Совершенно иного рода пример математической системы, в которой выполняются все формальные законы алгебры множеств, дается системой восьми чисел 1,2,3, 5, 6, 10, 15, 30: здесь а + b обозначает по определению общее наименьшее кратное а и b, ab - общий наибольший делитель а и b, a⊂b - утверждение "b делится на a" и a' - число 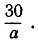Существование таких примеров повлекло за собой изучение общих алгебраических систем, удовлетворяющих законам 27). Такие системы называются "булевыми алгебрами" - в честь Джорджа Буля (1815-1864), английского математика и логика, книга которого "An investigation of the laws of thought" (Исследование законов мышления) появилась в 1854 г.