
3. Одно из применений к теории вероятностей
Алгебра множеств имеет ближайшее отношение к теории вероятностей и позволяет взглянуть на нее в новом свете. Рассмотрим простейший пример: представим себе эксперимент с конечным числом возможных исходов, которые все мыслятся как "равновозможные". Эксперимент может, например, заключаться в том, что мы вытягиваем наугад карту из хорошо перетасованной полной колоды. Если множество всех исходов эксперимента обозначим через I, а А обозначает какое-нибудь подмножество I, то вероятность того, что исход эксперимента окажется принадлежащим к подмножеству А, определяется как отношение
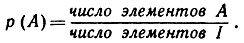
Если условимся число элементов в каком-нибудь множестве А обозначать через n(A), то последнему равенству можно придать вид:
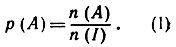
(1)
В нашем примере, допуская, что A есть подмножество треф, мы получим n(А) = 13,
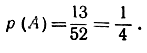
Идеи алгебры множеств обнаруживаются при вычислении вероятностей тогда, когда приходится, зная вероятности одних множеств, вычислять вероятности других. Например, зная вероятности р (А), р (В) и р (АВ), можно вычислить вероятность Р (А + В):
р (А + В) = р (А) + р (В) - р (АВ). (2),
Доказательство не представляет труда. Мы имеем:
n (А + В) = n (А) + n (В) - n (АВ),
так как элементы, содержащиеся одновременно в А и в В, т. е. элементы АВ, считаются дважды при вычислении суммы n (А) + n (В), и, значит, нужно вычесть n (АВ) из этой суммы, чтобы подсчет n (А + В) был произведен правильно. Деля затем обе части равенства на n (I), мы получаем соотношение (2).
Более интересная формула получается, если речь идет о трех множествах А, В, С из I. Пользуясь соотношением (2), имеем:
р (А + В + С) = р [(А + В) + С) = р (А + В) + р (С) - р [(А + В) С].
Закон (12) из предыдущего пункта дает нам: (А + В) С = АС + ВС. Отсюда следует
р [(А + В) С] = р (АС + ВС) = р (АС) + р (ВС) - р (ABC).
Подставляя в полученное раньше соотношение значение р [(А + В) С] и значение р (А + В), взятое из (2), мы приходим к нужной нам формуле:
р (А + В + С) = р(А) + р(В) + р (С) - р (АВ) - р (АС) - р (ВС) + р (ABC). (3)
В качестве примера рассмотрим следующий эксперимент. Три цифры 1, 2, 3 пишутся в каком попало порядке. Какова вероятность того, что по крайней мере одна из цифр окажется на надлежащем (в смысле нумерации) месте? Пусть А есть множество перестановок, в которых цифра 1 стоит на первом месте, В - множество перестановок, в которых цифра 2 стоит на втором месте, С - множество перестановок, в которых цифра 3 стоит на третьем месте. Нам нужно вычислить р (А + В + С). Ясно, что
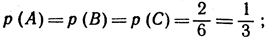
действительно, если какая-нибудь цифра стоит на надлежащем месте, то имеются две возможности переставить остальные две цифры из общего числа 3*2*1 = 6 возможных перестановок трех цифр. Далее,
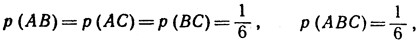
так как в каждом из этих случаев возникает только одна возможность. И тогда формула (3) дает нам
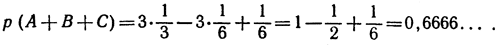
Упражнение. Вывести соответствующую формулу для р (A + В + С + D) и применить ее к эксперименту, в котором будут участвовать 4 цифры. Соответствующая вероятность равна 5/8 = 0,6250.
Общая формула для объединения n множеств имеет вид:
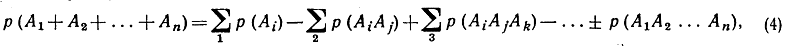
(4)
где символы 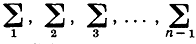 обозначают суммирование по всем возможным комбинациям, содержащим одну, две, три, ..., (n - 1) букв из числа А1, A2, ..., Аn. Эта формула может быть установлена посредством математической индукции - точно так же, как формула (3) была выведена из формулы (2).
обозначают суммирование по всем возможным комбинациям, содержащим одну, две, три, ..., (n - 1) букв из числа А1, A2, ..., Аn. Эта формула может быть установлена посредством математической индукции - точно так же, как формула (3) была выведена из формулы (2).
Из формулы (4) можно заключить, что если n цифр 1, 2, 3, ..., n написаны в каком угодно порядке, то вероятность того, что по крайней мере одна из цифр окажется на надлежащем месте, равна
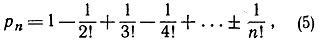
причем перед последним членом стоит знак + или -, смотря по тому, является ли n четным или нечетным. В частности, при n = 5 эта вероятность равна
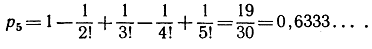
В главе VIII мы увидим, что, когда n стремится к бесконечности, выражение
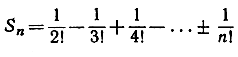
стремится к пределу 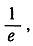 значение которого (с пятью знаками после запятой) равно 0,36788. Так как из формулы (5) видно, что рn = 1 - Sn, то отсюда следует, что при n→∞,
значение которого (с пятью знаками после запятой) равно 0,36788. Так как из формулы (5) видно, что рn = 1 - Sn, то отсюда следует, что при n→∞,
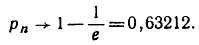
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'