Дополнение к главе II. Алгебра множеств

1. Общая теория

Понятие класса, или совокупности, или множества, объектов - одно из самых фундаментальных в математике. Множество определяется некоторым свойством ("аттрибутом") 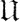, которым должен или обладать, или не обладать каждый рассматриваемый объект; те объекты, которые обладают свойством 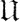, образуют множество А. Так, если мы рассматриваем целые числа и свойство 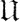заключается в том, чтобы "быть простым", то соответствующее множество А состоит из всех простых чисел 2, 3, 5, 7, ... .

Математическая теория множеств исходит из того, что из множеств с помощью определенных операций можно образовывать новые множества (подобно тому как из чисел посредством операций сложения и умножения получаются новые числа). Изучение операций над множествами составляет предмет "алгебры множеств", которая имеет много общего с обыкновенной числовой алгеброй, хотя кое в чем и отличается от нее. Тот факт, что алгебраические методы могут быть применены к изучению нечисловых объектов, каковыми являются множества, иллюстрирует большую общность идей современной математики. В последнее время выяснилось, что алгебра множеств бросает новый свет на многие области математики, например теорию меры и теорию вероятностей; она полезна также при систематизации математических понятий и выяснении их логических связей.

В дальнейшем I будет обозначать некоторое постоянное множество объектов, природа которых безразлична и которое мы можем называть универсальным множеством (или универсумом рассуждения), а А, В, С, ... будут какие-то подмножества I. Если I есть совокупность всех натуральных чисел, то А, скажем, может обозначать множество всех четных чисел, В - множество всех нечетных чисел, С - множество всех простых чисел и т. п. Если I обозначает совокупность всех точек на плоскости, то А может быть множеством точек внутри какого-то круга, В - множеством точек внутри другого круга и т. п. В число "подмножеств" нам удобно включить само I, а также "пустое" множество О, не содержащее никаких элементов. Цель, которую преследует такое искусственное расширение, заключается в сохранении того положения, что каждому свойству 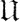соответствует некоторое множество элементов из I, обладающих этим свойством. В случае, если 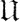есть универсально выполняемое свойство, примером которого может служить (если речь идет о числах) свойство удовлетворять тривиальному равенству х = х, то соответствующее подмножество I будет само I, так как каждый элемент обладает таким свойством; с другой стороны, если 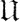есть какое-то внутренне противоречивое свойство (вроде х≠х), то соответствующее подмножество не содержит вовсе элементов, оно - "пустое" и обозначается символом О.

Говорят, что множество А есть подмножество множества В, короче, "A входит в B", или "В содержит A", если во множестве А нет такого элемента, который не был бы также во множестве В. Этому соотношению соответствует запись

Например, множество А всех целых чисел, делящихся на 10, есть подмножество множества В всех целых чисел, делящихся на 5, так как каждое число, делящееся на 10, делится также на 5. Соотношение А⊂В не исключает соотношения В⊂А. Если имеет место и то и другое, то мы пишем

Это означает, что каждый элемент А есть вместе с тем элемент В, и обратно, так что множества А и В содержат как раз одни и те же элементы.

Соотношение A⊂В между множествами во многих отношениях напоминает соотношение a≤b между числами. В частности, отметим следующие свойства этого соотношения:

1. A⊂A
2. Если A⊂В и В⊂А, то А = В.
3. Если A⊂В и В⊂С, то А⊂С.

По этой причине соотношение A⊂В иногда называют "отношением порядка". Главное отличие рассматриваемого соотношения от соотношения а≤b между числами заключается в том, что между всякими двумя заданными (действительными) числами а и b непременно осуществляется по меньшей мере одно из соотношений а≤b или b≤а, тогда как для соотношения А⊂В между множествами аналогичное утверждение неверно. Например, если А есть множество, состоящее из чисел 1, 2, 3:

а В - множество, состоящее из чисел 2, 3 4:

то не имеет места ни соотношение A⊂В, ни соотношение В⊂А. По этой причине говорят, что подмножества А, В, С, ... множества I являются "частично упорядоченными", тогда как действительные числа а, b, с, ... образуют "линейно упорядоченную" совокупность.

Заметим, между прочим, что из определения отношения A⊂В следует, что, каково бы ни было подмножество А множества I,

и

Свойство 4) может показаться несколько парадоксальным, но, если вдуматься, оно логически строго соответствует точному смыслу определения знака ⊂. В самом деле, соотношение О⊂А нарушалось бы только в том случае, если бы пустое множество О содержало элемент, который не содержался бы в A; но так как пустое множество не содержит вовсе элементов, то этого быть не может, каково бы ни было А.

Мы определим теперь две операции над множествами, формально обладающие многими алгебраическими свойствами сложения и умножения чисел, хотя по своему внутреннему содержанию совершенно отличные от этих арифметических действий. Пусть А и В - какие-то два множества. Под объединением, или "логической суммой", А и В понимается множество, состоящее из тех элементов, которые содержатся или в А, или в В (включая и те элементы, которые содержатся и в А и в В). Это множество обозначается А + В^*. Под пересечением, или "логическим произведением", А и В понимается множество, состоящее из тех элементов, которые содержатся и в А и в В. Это множество обозначается АВ^**. Проиллюстрируем приведенные определения примером. Возьмем опять в качестве А и В множества

^* (Или А∪B.)

^** (Или А∩B.)

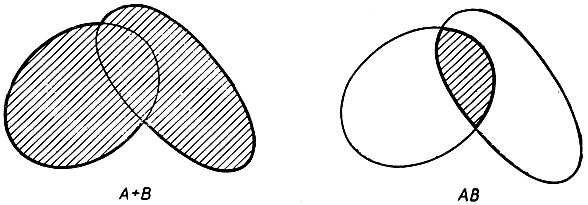
Рис. 26. Объединение и пересечение множеств

Тогда

Среди важных алгебраических свойств операций А + В и АВ перечислим следующие. Читатель сможет проверить их справедливость, исходя из определения самих операций:

Проверка всех этих законов - дело самой элементарной логики. Например, правило 10) констатирует, что множество элементов, содержащихся или в A, или в A, есть как раз множество A; правило 12) констатирует, что множество тех элементов, которые содержатся в A и вместе с тем содержатся в В или в С, совпадает со множеством элементов, которые содержатся одновременно в A и в В или содержатся одновременно в A и в С. Логические рассуждения, используемые при доказательствах подобного рода правил, удобно иллюстрируются, если мы условимся изображать множества A, В, С, . . .в виде некоторых фигур на плоскости и будем очень внимательны в том отношении, чтобы не упустить ни одной из возникающих логически возможностей, когда речь идет о наличии общих элементов двух множеств или, напротив, наличии в одном множестве элементов, которые не содержатся в другом.

Читатель, несомненно, обратил внимание на то обстоятельство, что законы 6), 7), 8), 9) и 12) внешне тождественны с хорошо знакомыми коммутативным, ассоциативным и дистрибутивным законами обыкновенной алгебры. Отсюда следует, что все правила обыкновенной алгебры, вытекающие из этих законов, действительны также в алгебре множеств. Напротив, законы 10), 11) и 13) не имеют своих аналогов в обыкновенной алгебре, и они придают алгебре множеств более простую структуру. Например, формула бинома в алгебре множеств сводится к простейшему равенству

которое следует из закона 11). Законы 14), 15) и 17) говорят о том, что свойства множеств О и I по отношению к операциям объединения и пересечения множеств весьма похожи на свойства чисел 0 и 1 по отношению к операциям числовых действий сложения и умножения. Но закон 16) не имеет аналога в числовой алгебре.

Остается дать определение еще одной операции в алгебре множеств. Пусть A - какое-нибудь подмножество универсального множества I. Тогда под дополнением А в I понимается множество всех элементов I, которые не содержатся в A. Для этого множества мы введем обозначение А'. Так, если I есть множество всех натуральных чисел, а A - множество всех простых чисел, то А' есть множество, состоящее из всех составных чисел и числа 1. Операция перехода от A к A', для которой нет аналога в обыкновенной алгебре, обладает следующими свойствами:

Проверку этих свойств мы опять предоставляем читателю.

Законы 1)-26) лежат в основе алгебры множеств. Они обладают следующим замечательным свойством "двойственности":

Если в каком-либо из законов 1)-26) заменить друг на друга соответственно символы

(в каждом их вхождении), то в результате снова получится один из этих же законов. Например, закон 6) переходит в закон 7), 12)- в 13), 17)- в 16) и т. д. Отсюда следует, что каждой теореме, которая может быть выведена из законов 1)-26), соответствует другая, "двойственная" ей теорема, получающаяся из первой посредством указанных перестановок символов. В самом деле, так как доказательство первой теоремы состоит из последовательного применения (на различных стадиях проводимого рассуждения) некоторых из законов 1)-26), то применение на соответствующих стадиях "двойственных" законов составит доказательство "двойственной" теоремы. (По поводу подобной же "двойственности" в геометрии см. главу IV.)