**2. Теорема Лиувилля и конструирование трансцендентных чисел

Доказательство существования трансцендентных чисел еще до Кантора было дано Ж. Лиувиллем (1809-1862). Оно дает возможность на самом деле конструировать примеры таких чисел. Доказательство Лиувилля более трудно, чем доказательство Кантора, и это не удивительно, так как сконструировать пример, вообще говоря, сложнее, чем доказать существование. Приводя ниже доказательство Лиувилля, мы имеем в виду только подготовленного читателя, хотя для понимания доказательства совершенно достаточно знания элементарной математики.

Как обнаружил Лиувилль, иррациональные алгебраические числа обладают тем свойством, что они не могут быть приближены рациональными числами с очень большой степенью точности, если только не взять знаменатели приближающих дробей чрезвычайно большими.

Предположим, что число z удовлетворяет алгебраическому уравнению с целыми коэффициентами

но не удовлетворяет такому же уравнению более низкой степени. Тогда говорят, что само х есть алгебраическое число степени n. Так, например, число z = √2 есть алгебраическое число степени 2, так как удовлетворяет уравнению х² - 2 = 0 степени 2, но не удовлетворяет уравнению первой степени; число 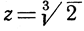- степени 3, так как удовлетворяет уравнению х³ - 2 = 0, но не удовлетворяет (как мы покажем в главе III) уравнению более низкой степени. Алгебраическое число степени n>1 не может быть рациональным, так как рациональное число 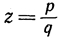удовлетворяет уравнению qx - р = 0 степени 1. Каждое иррациональное число z может быть с какой угодно степенью точности приближено с помощью рационального числа; это означает, что всегда можно указать последовательность рациональных чисел

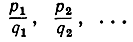
с неограниченно растущими знаменателями, обладающую тем свойством, что

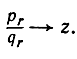
Теорема Лиувилля утверждает: каково бы ни было алгебраическое число z степени n>1, оно не может быть приближено посредством рационального числа 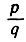с точностью, лучшей чем 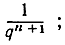другими словами, при достаточно больших знаменателях непременно выполняется неравенство

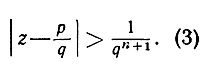
Мы собираемся привести доказательство этой теоремы, но раньше покажем, как с ее помощью можно строить трансцендентные числа. Рассмотрим число

где а_i обозначают произвольные цифры от 1 до 9 (проще всего было бы положить все а_i равными 1), а символ n!, как обычно (см. стр. 42), обозначает 1*2*...*n. Характерным свойством десятичного разложения такого числа является то, что быстро возрастающие по своей длине группы нулей чередуются в нем с отдельными цифрами, отличными от нуля. Обозначим через z_m конечную десятичную дробь, получающуюся, когда в разложении возьмем все члены до а_m*10^-m! включительно. Тогда получим неравенство

Предположим, что z было бы алгебраическим числом степени n. Тогда, полагая в неравенстве Лиувилля (3) 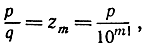мы должны иметь

|z - z_m|>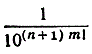

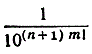
при достаточно больших значениях т. Сопоставление последнего неравенства с неравенством (4) дает

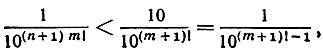
откуда следует (n + 1)m!>(m + 1)! - 1 при достаточно больших m. Но это неверно для значений m, больших чем n (пусть читатель потрудится дать подробное доказательство этого утверждения). Мы пришли к противоречию. Итак, число z - трансцендентное.

Остается доказать теорему Лиувилля. Предположим, что z - алгебраическое число степени n>1, удовлетворяющее уравнению (1), так что

Пусть 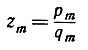последовательность рациональных чисел, причем z_m → z.

Тогда

Деля обе части на z_m - z и пользуясь алгебраической формулой

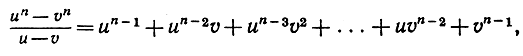
мы получаем:

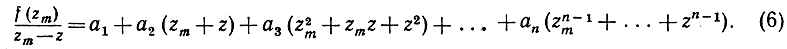
(6)

Так как z_m стремится к z, то при достаточно больших m рациональное число z_m будет отличаться от z меньше, чем на единицу. Поэтому при достаточно больших m можно сделать следующую грубую оценку:

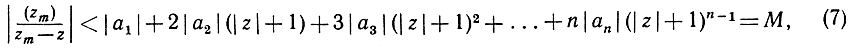
(7)

причем стоящее справа число М постоянное, так как z не меняется в процессе доказательства. Выберем теперь m настолько большим, чтобы у дроби 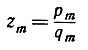знаменатель q_m был больше, чем М; тогда

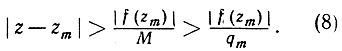
(8)

Ради краткости условимся дальше писать р вместо р_m и q вместо q_m. В таком случае

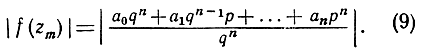
(9)

Рациональное число 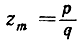не может быть корнем уравнения f(x) = 0, так как тогда можно было бы из многочлена f(x) выделить множитель (х - z_m), и, значит, z удовлетворяло бы уравнению степени, низшей чем n. Итак, f(z_m)≠0. Но числитель в правой части равенства (9) есть целое число и, следовательно, по абсолютному значению он по меньшей мере равен единице. Таким образом, из сопоставления соотношений (8) и (9) вытекает неравенство

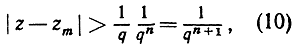
(10)

как раз и составляющее содержание указываемой теоремы.

На протяжении нескольких последних десятилетий исследования, касающиеся возможности приближения алгебраических чисел рациональными, были продвинуты гораздо дальше. Например, норвежский математик А. Туэ (1863-1922) установил, что в неравенстве Лиувилля (3) показатель n+1 может быть заменен меньшим показателем 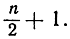К. Л. Зигель показал, что можно взять и еще меньший (еще меньший при больших n) показатель 2√n.

Трансцендентные числа всегда были темой, приковывающей к себе внимание математиков. Но до сравнительно недавнего времени среди чисел, которые интересны сами по себе, было известно очень немного таких, трансцендентный характер которых был бы установлен. (В главе III будет доказана трансцендентность числа я, и отсюда будет следовать невозможность квадратуры круга с помощью линейки и циркуля.) В своем выступлении на Парижском международном математическом конгрессе 1900 г. Давид Гильберт предложил тридцать математических проблем, допускающих простую формулировку, некоторые - даже совсем элементарную и популярную, из которых ни одна не только не была решена, но даже и не казалась способной быть разрешенной средствами математики той эпохи. Эти "проблемы Гильберта" оказали сильное возбуждающее влияние на протяжении всего последующего периода развития математики. Почти все они мало-помалу были разрешены, и во многих случаях их решение было связано с ясно выраженными успехами в смысле выработки более общих и более глубоких методов. Одна из проблем, казавшаяся довольно безнадежной, заключалась в доказательстве того, что число

является трансцендентным (или хотя бы иррациональным). На протяжении трех десятилетий не было даже намека на такой подход к вопросу с чьей-нибудь стороны, который открывал бы надежду на успех. Наконец, Зигель и, независимо от него, молодой русский математик А. Гельфонд открыли новые методы для доказательства трансцендентности многих чисел, имеющих значение в математике. В частности, была установлена трансцендентность не только гильбертова числа 2^√2, но и целого довольно обширного класса чисел вида а^b, где а - алгебраическое число (&38800;0 и ≠1), а b - иррациональное алгебраическое число.