
3. Формула Муавра и корни из единицы
Под корнем n-й степени из числа a мы понимаем всякое такое число b, что bn = а. В частности, число 1 имеет два квадратных корня: 1 и -1, так как 12 = (-1)2 = 1. Число 1 имеет один действительный кубический корень, именно 1, тогда как оно же имеет четыре корня четвертой степени: два действительных 1 и -1 и два мнимых i и -i. Эти факты наводят на мысль, что в комплексной области должно существовать еще два кубических корня из 1 (а всего кубических корней тогда будет три). С помощью формулы Муавра мы покажем, что эта догадка справедлива.
Мы убедимся, что в поле комплексных чисел существует ровно n корней степени n из 1. Эти корни изображаются вершинами правильного n-угольника, вписанного в единичный круг и имеющего точку 1 в качестве одной из вершин.
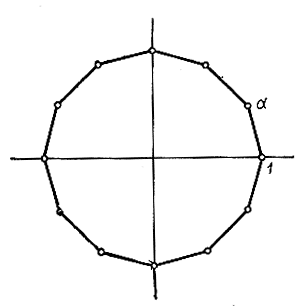
Рис. 25. Двенадцать корней двенадцатой степени из единицы
Сказанное почти ясно из рис. 25 (соответствующего случаю n = 12). Первая вершина многоугольника есть 1. Следующая есть
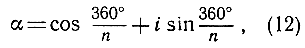
(12)
так как аргумент должен равняться n-й части угла в 360°. Следующая вершина есть α*α= α2, так как мы получим ее, вращая вектора α на угол 360°/n. Дальше получаем вершину α3 и т. д.; после п шагов возвращаемся снова к вершине 1, т. е. получаем
αn = 1,
что следует также из формулы (11), так как

Итак, α1 = α есть корень уравнения xn = 1. То же справедливо относительно следующей вершины
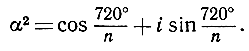
Мы убедимся в этом, если напишем
(α2)n = α2n = (αn)2 = 12 = 1,
или же воспользуемся формулой Муавра
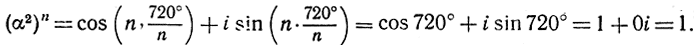
Точно так же мы заключаем, что все n чисел
1, α, α2, α3, ..., αn-1
являются корнями степени n из 1. Если будем степени увеличивать дальше или рассмотрим отрицательные степени, то новых корней не получим. В самом деле,
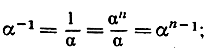
точно так же αn = 1, αn+1 = (αn)α = 1*α = α и т. д., так что ранее полученные корни повторяются. Читателю предоставляем в качестве упражнения показать, что иных корней, кроме перечисленных, рассматриваемое уравнение не имеет.
Если n - четное, то одна из вершин n-угольника попадает в точку -1 в соответствии с общеизвестным алгебраическим фактом: -1 есть корень четной степени из 1.
Уравнение, которому удовлетворяют корни n-й степени из 1,
хn - 1 = 0, (13)
есть уравнение n-й степени; но легко понизить его степень на единицу. Воспользуемся алгебраической формулой
(xn - 1) = (x - 1)(xn-1 + xn-2 + xn-3 + ... + 1)(14)
Так как произведение двух чисел равно 0 в том и только в том случае, если один из множителей равен нулю, то выражение (14) обращается в нуль или при x = 1, или при условии, что удовлетворяется уравнение
xn-1 + xn-2 + xn-3 + ... x + 1 = 0 (15)
Этому уравнению удовлетворяют корни α, α2, ..., αn-1; оно называется циклотомическим, или уравнением деления окружности. Так, например, мнимые кубические корни из 1
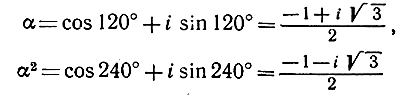
являются корнями уравнения
x2 + x + 1 = 0,
как читатель сможет убедиться, выполняя подстановки. Таким же образом корни пятой степени из 1 (кроме самого числа 1) удовлетворяют уравнению
х4 + x3 + х2 + х + 1 = 0. (16)
Чтобы построить правильный пятиугольник, нам приходится решить уравнение четвертой степени, Простое алгебраическое ухищрение - замена 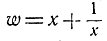 приводит к уравнению второй степени. Мы делим уравнение (16) на х2 и переставляем члены:
приводит к уравнению второй степени. Мы делим уравнение (16) на х2 и переставляем члены:
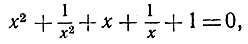
и, принимая во внимание, что 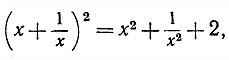 получаем:
получаем:
ω2 + ω - 1 = 0.
По формуле (7) пункта 1 корни этого квадратного уравнения имеют вид.
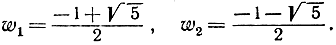
Итак, мнимые корни пятой степени из 1 являются корнями следующих двух квадратных уравнений:
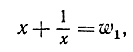
или
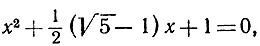
и
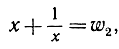
или
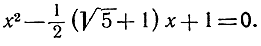
Читатель сможет их решить по той же формуле (7).
Упражнения.
- Найти корни 6-й степени из 1.
- Вычислить (1 + i)11.
- Вычислить все различные значения выражений
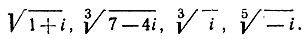
- Вычислить
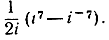
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'